Authors:
(1) Wahei Hara;
(2) Yuki Hirano.
Table of Links
- Abstract and Intro
- Exchanges and Mutations of modifying modules
- Quasi-symmetric representation and GIT quotient
- Main results
- Applications to Calabi-Yau complete intersections
- Appendix A. Matrix factorizations
- Appendix B. List of Notation
- References
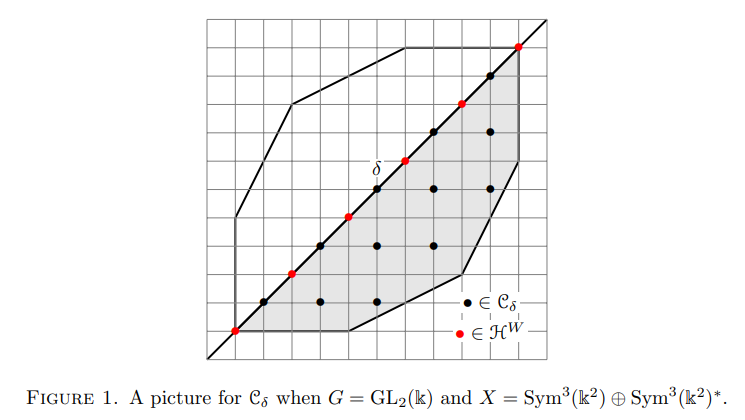
3. Quasi-symmetric representation and GIT quotient
3.1. Quasi-symmetric representations and magic windows. This section recalls fundamental properties of derived categories of GIT quotients arising from quasi-symmetric representations, which are established in [HSa] and [SV1]. We freely use notation from Section 1.6.

and then it associates the GIT quotient stack [Xss(ℓ)/G].

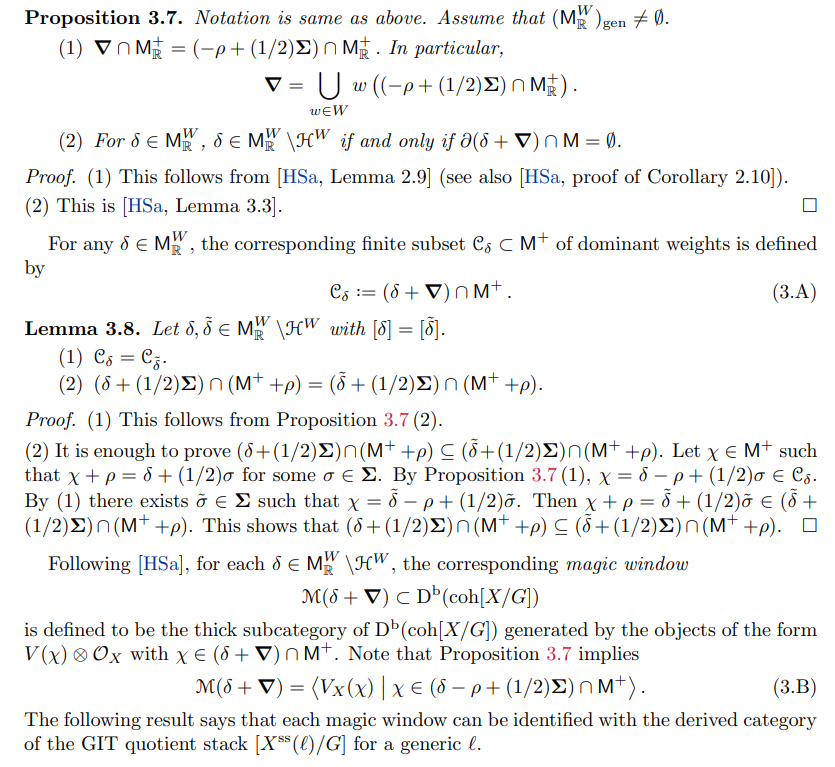

Proposition 3.10 ([HSa, Proposition 6.2]). There is an equivalence of groupoids
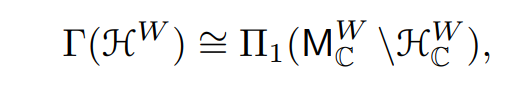
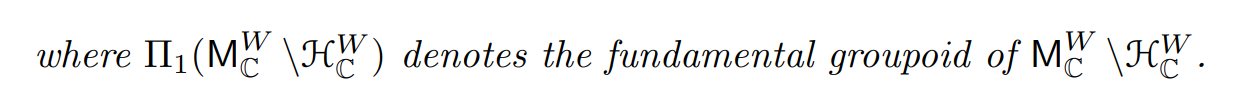




Proposition 3.13 ([HSa, Proposition 6.5]). There is an equivalence
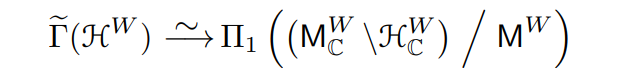
extending the equivalence in Proposition 3.10.


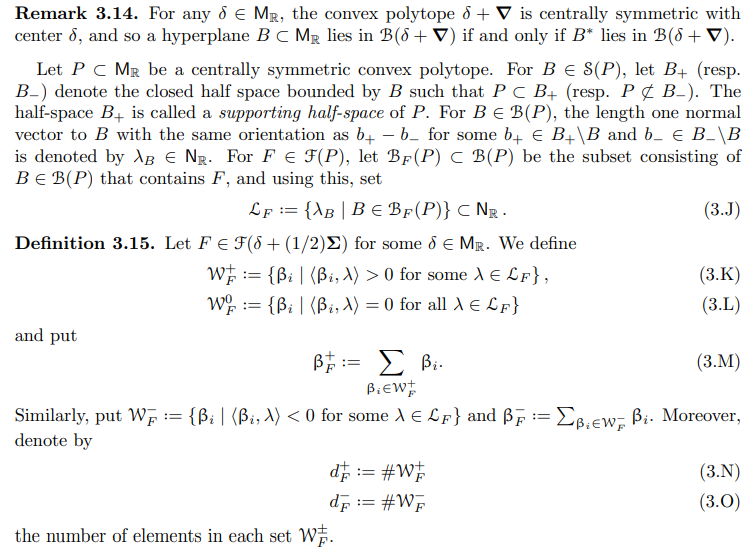
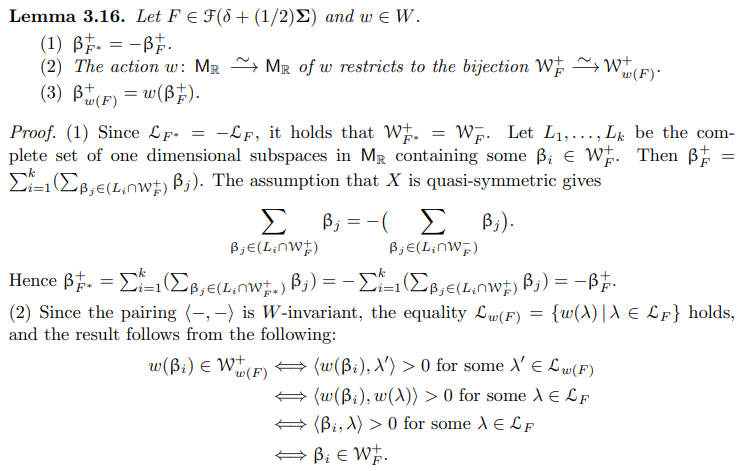
(3) This follows from (2).
The following is elementary, but we give a proof for the convenience of the reader


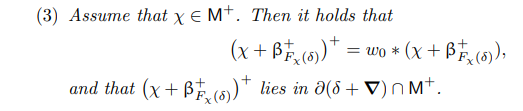
Proof. If W is trivial, the results are obvious. Thus, assume that W ̸= 1

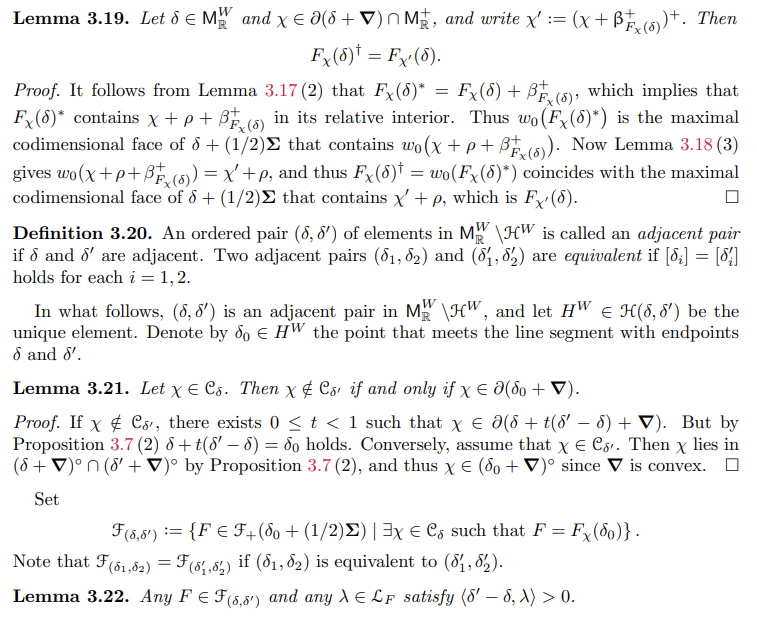
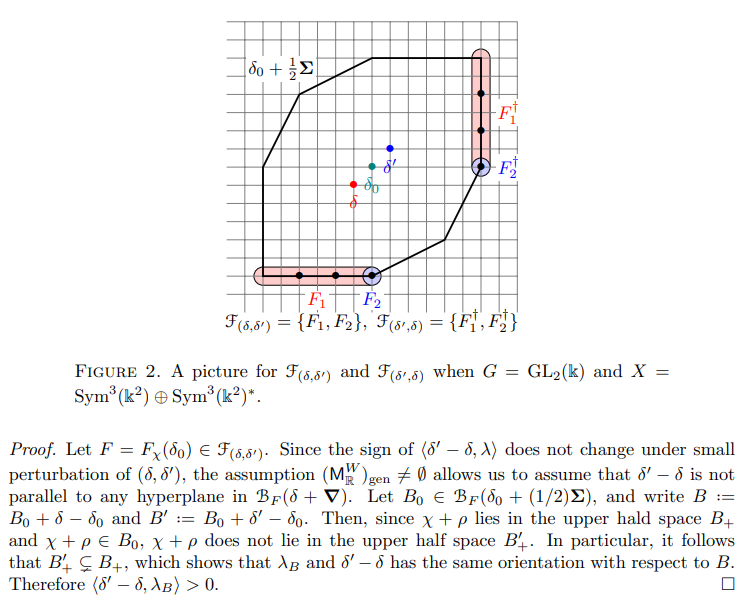

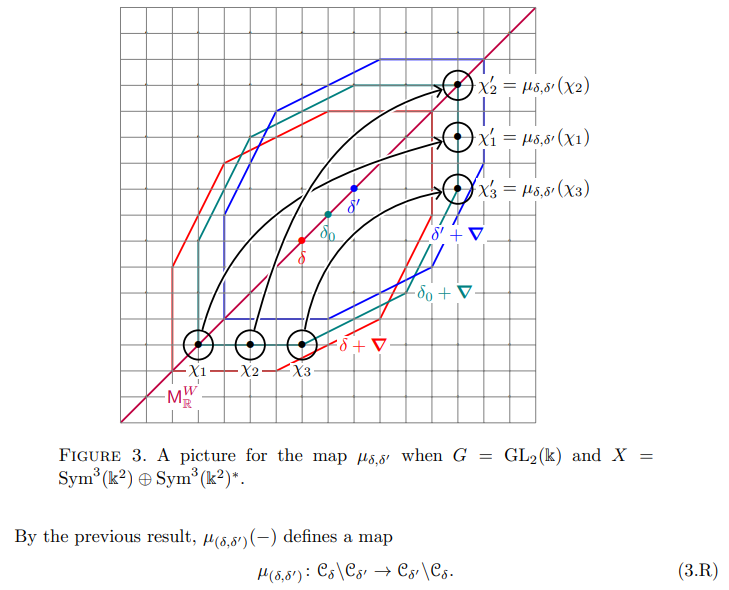
The following result proves that this map is bijective.
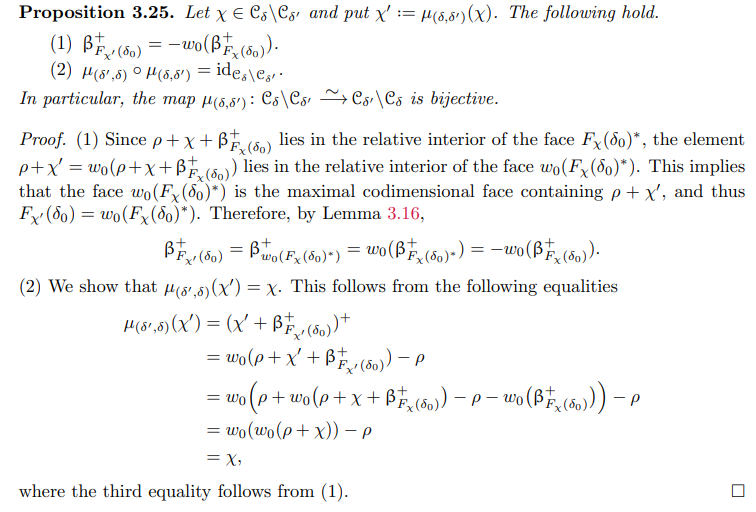



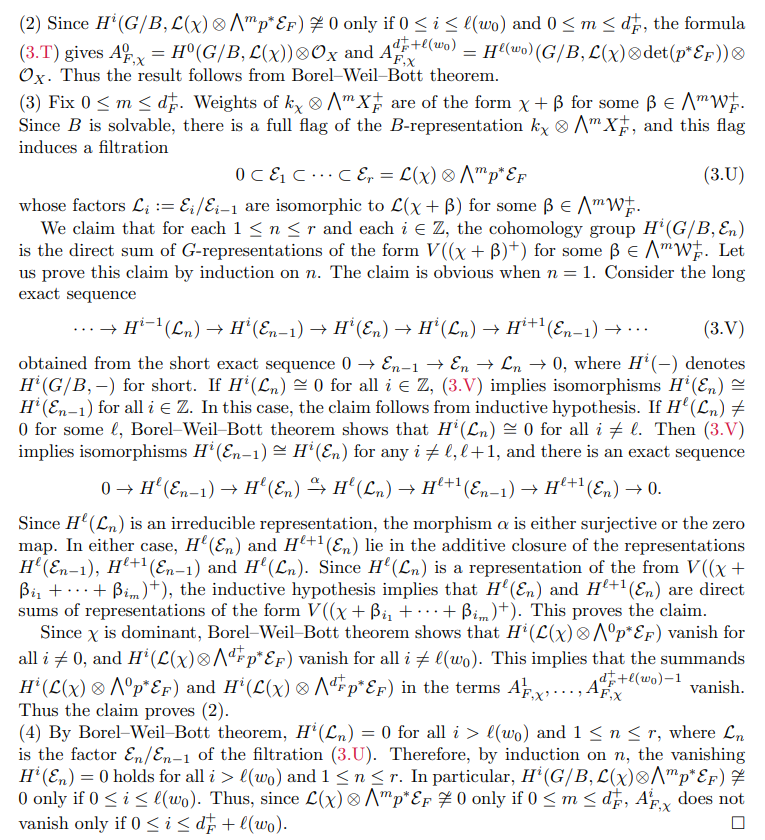
This paper is available on arxiv under CC0 1.0 DEED license.

