This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Vitor da Fonseca, Instituto de Astrof´ısica e Ciˆencias do Espa¸co, Faculdade de Ciˆencias da Universidade de Lisboa;
(2) Tiago Barreiro, Instituto de Astrof´ısica e Ciˆencias do Espa¸co, Faculdade de Ciˆencias da Universidade de Lisboa and 2ECEO, Universidade Lus´ofona;
(3) Nelson J. Nunes, Instituto de Astrof´ısica e Ciˆencias do Espa¸co, Faculdade de Ciˆencias da Universidade de Lisboa.
Table of Links
- Abstract and Intro
- Coupling Dark Energy to Neutrinos
- Impact of the Coupling on Perturbations and Observables
- Parameter Estimation
- Discussion
- Acknowledgment, Appendix, and References
III. IMPACT OF THE COUPLING ON PERTURBATIONS AND OBSERVABLES
A. Perturbation equations

The perturbed energy density and pressure of the interacting neutrinos have been derived in previous studies (see e.g. [16, 19, 20]):

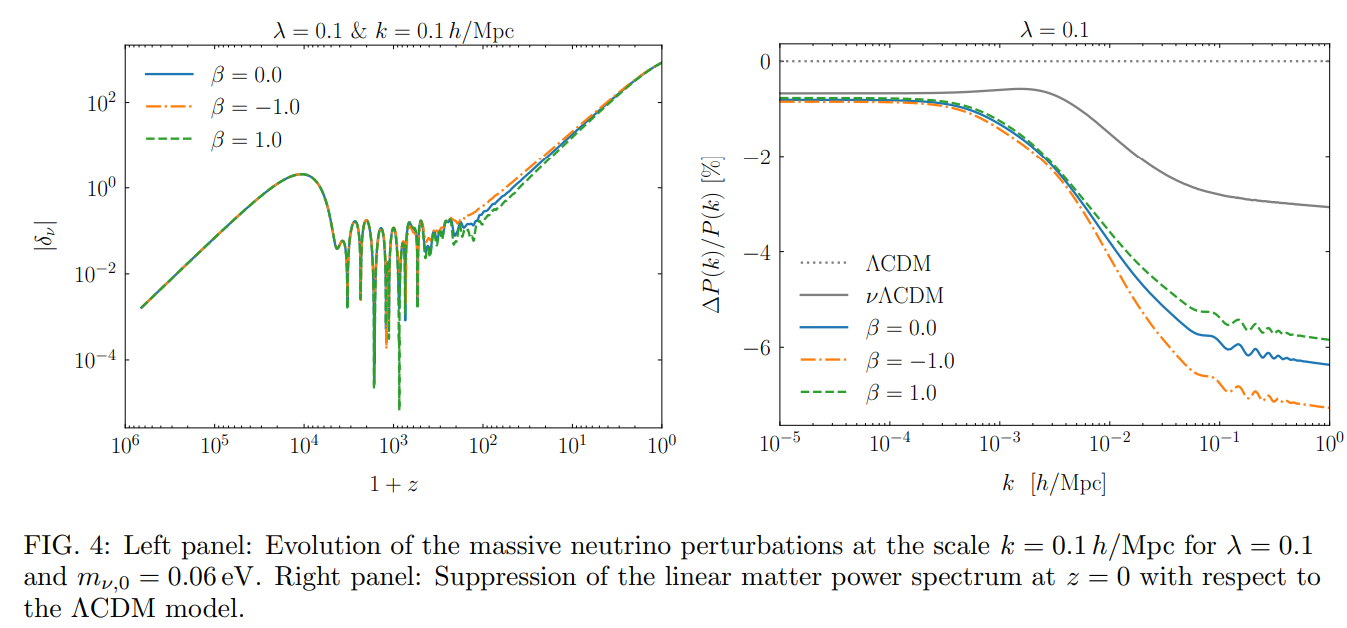


where the neutrino anisotropic stress σν [46] is not changed by the coupling. We have adjusted the fluid approximation equations of the non cold dark matter in the CLASS code accordingly
Deep in the non-relativistic regime, when wν = 0, the ratio q/ϵ vanishes asymptotically and the pressure perturbations in the neutrino fluid, as well as the shear stress, become negligible with respect to density perturbations. The continuity and Euler equations are analogous to those of the coupled cold dark matter model [26, 48],
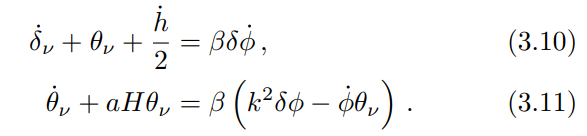
For to the coupled scalar field, the equation of motion of the fluctuations is the following,
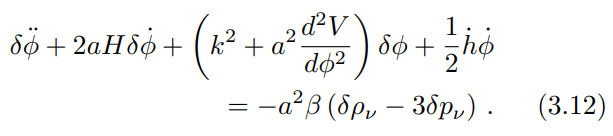
As in the background, we evolve the field perturbations with the potential through the above equation in our version of the CLASS code.
B. Effects on the matter power spectrum
There are three main stages of the evolution of the neutrino density contrast affected by the coupling. During the radiation-dominated era, when the neutrinos are decoupled from the thermal bath but still relativistic, their perturbations grow as radiation. Later, the neutrinos become non-relativistic and cluster in the gravitational potential wells of cold dark matter, which is the dominant cosmological component. However, below their free-streaming scale, they do not cluster like cold dark matter [1]. Neutrino free streaming dampens the neutrino fluctuations up to a critical scale depending on the neutrino mass, and giving the oscillatory pattern seen in the left panel of Fig. 4. The free-streaming wavenumber of Fourrier mode reaches a minimum at the nonrelativistic transition, given by [2]
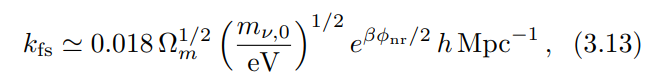
during matter or dark energy domination. Or equivalently, using Eqs. (2.22) and (2.23), we get
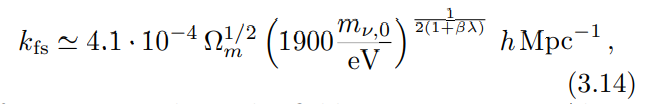
for our particular scalar field parametrization. Above the free-streaming length, the neutrino fluctuations grow unhindered. For growing neutrino masses (β > 0, green dashed line) the free-streaming scale in Eq.(3.14) is larger and the growth of the fluctuations is delayed with respect to shrinking neutrino masses (β < 0, orange dash-dotted line).
Furthermore, the dependence of the neutrino mass on β changes the fraction of matter whose fluctuations do not grow like cold dark matter at a given scale. The neutrinos do not contribute to the creation of potential wells below the free streaming scale, and all structure formation is damped because the gravitational wells are not as deep as they would be in the presence of only non-relativistic matter.

Moreover, the non-negligible fraction of dark energy itself (λ ̸= 0 and β = 0, blue solid line) further reduces the growth of the fluctuations during matter dominance, leading to more power suppression. On the other hand, the matter power spectrum at small scales also depends on how large the neutrino mass was in the past. Growing neutrino masses (β > 0, green dashed line) reduce the power suppression caused by the scalar field, while shrinking neutrino masses increase the suppression (β < 0, orange dash-dotted line).
D. Effects on the CMB lensing potential
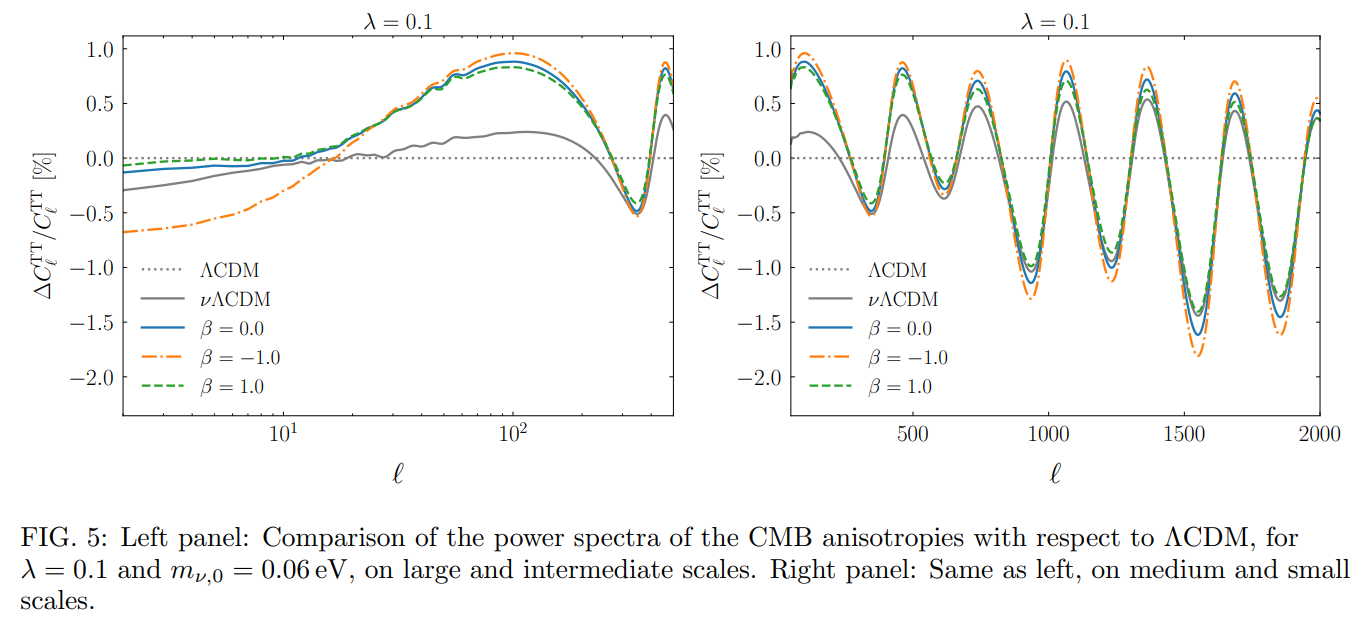
Because the free-streaming neutrinos erase the density perturbations, they affect the CMB light which is distorted by the gravitational lensing caused by the intervening matter distribution between us and the last scattering surface [49]. The neutrinos reduce the CMB lensing potential, which is a measure of the integral of the gravitational potentials along the line of sight between the recombination time and the present time. The effect of the weak lensing is to smooth the power spectrum of the CMB temperature anisotropies on small scales. Note in Fig. 6 that since the effect is proportional to the energy density of the neutrinos, it can constrain their mass, whose cosmological evolution is controlled by the two parameters λ and β. For example, if the neutrino mass had been too high in the recent past, we would have had less lensing than we observe. The suppression already caused by the scalar field (β = 0, blue solid curve) is either enhanced by shrinking neutrino masses (β < 0, orange dash-dotted line) or compensated by growing neutrino masses (β > 0, green dashed line).
It is worth noting that, in contrast to the modelindependent parametrization for the neutrino mass variation studied in Ref. [20], we do not find instabilities on large scales in our model [50], which would be triggered by large coupling values causing the neutrino perturbations to grow rapidly on the largest scales observable.