How Strategic Traders Disrupt Auction Efficiency—and What to Do About It

Table of Links

Abstract

1. Introduction

   1.1 Periodic auction and continuous limit order book

   1.2 Comparison and main flaws of limit order book

   1.3 Optimal policies to cure auction’s inefficiencies and related works

2. Auctions market modeling with transaction fees and randomization

   2.1 The market characteristics

   2.2 Clearing Price rule

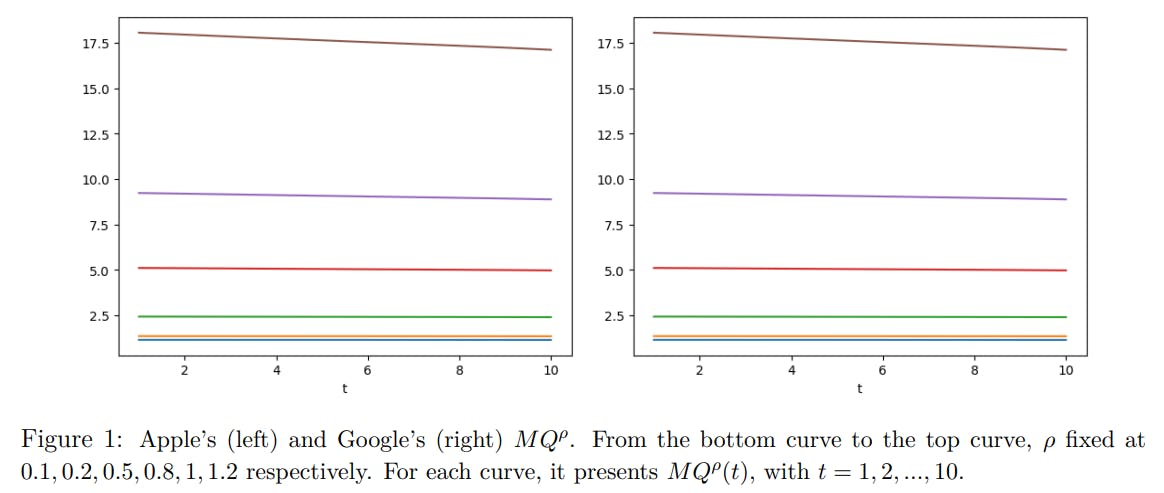
   2.3 Strategic Trader’s optimization and market quality

   2.4 Data and numerical analysis

   2.5 Strategic trader with full information: efficient but unfair market

   2.6 Imperfect information and inefficiency of auctions

3. Monitoring policies: transaction fees and clearing time randomization

   3.1 Bilevel optimization between the exchange and the strategic trader

   3.2 Randomization without fees

   3.3 Optimal transaction fees indexed on time to improve price impact for the trader

   3.4 Optimal transaction fees indexed on time: improving market quality while benefiting from the fees

4. Conclusions

A. Appendix: Numerical Methods

A.1 Problem of a Strategic Seller

A.2 Appendix: Problem of the Regulator

B Appendix: Illustrate Remark 2.4

References

1.3 Optimal policies to cure auction’s inefficiencies and related works

In this paper, we are interested in furthering the design of AHEAD, the concurrence of a continuous market and a periodic auction market, and we focus specifically on the periodic auction part. We want to see whether a strategic trader could take advantage of the current setting when an auction is open. The main question raising our motivation is the following.

Would a strategic player disturbs market efficiency by strategically picking their arrival time? If so, how could we improve the auction design to bring back efficiency?

The efficiency measure we use is a price discovery measure, the difference between the actual clearing price of an asset and its theoretical efficient price. To get a larger picture, “market efficiency” usually refers to either “external efficiency” or “internal efficiency” (see [West (1975)]). A market is externally efficient if its prices reflect all available information. Fama develops this definition in [Fama (1970)] (also see [Malkiel (2003)]). Relevant criteria to measure the market quality include auto-correlation of return, delay measure, and Sharpe ratio (see [Griffin et al. (2010)] and [Liu and Chen (2020)]). . . . Such efficiency is called external because it depends not on trading systems but on the outside world, such as how information is spread among traders. Internal efficiency refers to whether a market could enable traders to trade at prices close enough to their desired prices. The difference could be generated by the distance between the executed price and the true price (also called pricing error, price discovery measure, or price formation measure) and by transaction costs such as liquidation and bid-ask spread. We adopt the price discovery measure because it suits our purpose the most and because most relevant work uses such measure (see all relevant work cited in the introduction and see [Madhavan (1992)]).

The main results of our paper are as following. By studying the behavior of a strategic trader in a periodic auction, we emphasize that the trader benefit from arriving only at the end of an auction and right before the auction closes. Such strategic choice of arrival time enables the trader to take advantage of all known information to submit a strategic price and have the greatest price impact on the market. Not only is such strategic timing unfair to other market participants, but also the strategic pricing could drive the clearing price away from the efficient price of the underlying asset if the strategic trader has an incorrect guess about the efficient price. It can be seen as a disturbance to market efficiency.

We propose two regulatory policies to respond to this mechanical problem inherent in periodic auction markets. First, we introduce a randomization design of the auction’s closing time. Second, we introduce a transaction fee indexed on the arrival time of a strategic trader in the auction, i.e., the later a trader arrives, the higher they pay. We prove that the randomization and the transaction fee design address the problem efficiently and bring better quality to the market. Note that the randomization of the closing time is mentioned in [Farmer and Skouras (2012)] and [Wah et al. (2016)]. However, none of these works study the possible effects of such design and use quantification methods to address it. In reality, randomization of closing time is implemented, so it is possible to conduct an empirical analysis of such a design. London Stock Exchange adds a 30-second random period to the opening auction and closing auction. Cboe randomizes the whole duration of its periodic auction, i.e., an auction might close in 0 to 100 milliseconds. However, we caution that any conclusions on empirical analysis of real-world auction design might not apply to auction design because real-world auctions have specific settings, including auction duration and priority rules. Excluding or changing any of the settings could lead to a different conclusion.

Additionally, we would like to remind that our model of a periodic auction adopts the most basic set of rules. Periodic auction markets in reality could be much more complicated. Apart from Cboe’s priority rule we mentioned above, the opening and closing auction of NYSE and Nasdaq each add their own matching and execution rules. These rules could possibly limit many advantages of a periodic auction market; see [Jegadeesh and Wu (2022)] for an empirical analysis of NYSE and Nasdaq’s closing auctions.

The structure of this study is the following. In Section 2, we introduce the auction mechanism and the modeling without fees or randomization. Section 2 presents the main charcateristics of the market, the mathematical model and the information set available for the strategic trader. Section 2.1 set the clearing price rule to trade the considered asset ensuring the largest number of matching orders (see Proposition 2.1). Section 2.3 define the optimization problem of the strategic trader without regulation (randomization of the clearing time and transaction fees) together with its impact of the market quality. Section 2.4 introduce the data set together with the calibration of the relevant parameters for the study. Section 2.5 presents the solution of the problem when the strategic trader has a full information on the traded asset illustrated with numerical results. Section 2.6 studies the case where the strategic trader is imperfectly informed about the efficient price of the asset. Section 3 turns to the impact of a clearing time randomization and transaction fees policy on the strategic trader behavior, the price impact and the market quality. The bilevel optimization is first introduced, following by the result considering only a randomization of the clearing time without fees then adding the fees. We consider two different problems from the exchange perspective to improve the market quality: either to reduce the price impact including the fees paid by the trader (Section 3.3) or to reduce the distance between the clearing price and the efficient price while benefiting from the fees structure (Section 3.4). Section 4 concludes the study and provides future perspective.