New Concentration Inequalities for Availability‑Throughput Tradeoffs with Applications in Economics

Table of Links

Abstract and 1. Introduction

2. The Soup Kitchen Problem

   2.1 Model and 2.2 Limits of Throughput and Availability

   2.3 Analysis of Throughput and Availability

3. Multi-Unit Posted-Price Mechanisms

   3.1 Model

   3.2 Results

4. Transaction fee mechanism design

5. Conclusions and future work, and References

A. Proofs for Section 2 (The Soup Kitchen Problem)

B. Proofs for Section 3 (Multi-Unit Posted-Price Mechanisms)

Abstract

This paper studies the fundamental limits of availability and throughput for independent and heterogeneous demands of a limited resource. Availability is the probability that the demands are below the capacity of the resource. Throughput is the expected fraction of the resource that is utilized by the demands. We offer a concentration inequality generator that gives lower bounds on feasible availability and throughput pairs with a given capacity and independent but not necessarily identical distributions of up-to-unit demands. We show that availability and throughput cannot both be poor. These bounds are analogous to tail inequalities on sums of independent random variables, but hold throughout the support of the demand distribution. This analysis gives analytically tractable bounds supporting the unit-demand characterization of Chawla, Devanur, and Lykouris (2023) and generalizes to up-to-unit demands. Our bounds also provide an approach towards improved multi-unit prophet inequalities (Hajiaghayi, Kleinberg, and Sandholm, 2007). They have applications to transaction fee mechanism design (for blockchains) where high availability limits the probability of profitable user-miner coalitions (Chung and Shi, 2023).

1 Introduction

Consider the following Soup Kitchen Problem:

A soup kitchen produces κ units of soup, and serves diners with independent but not necessarily identically distributed demands of at most one unit. An auditor needs to ensure that the soup kitchen is performing well. Two key performance metrics are availability α and throughput τ . Availability is the probability the kitchen does not run out of soup. Throughput is the expected fraction of soup produced that is consumed. The auditor’s problem is to catch an underperforming soup kitchen by establishing a lower bound on feasible availability and throughput pairs.

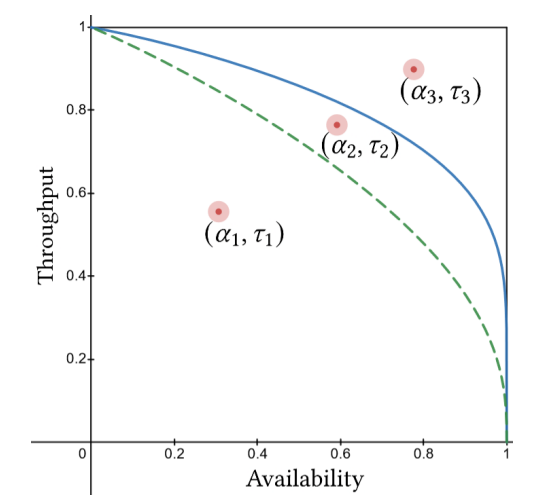
Both throughput and availability are important. If a soup kitchen has low throughput, much of the soup produced each day goes to waste. However, if it has low availability, prospective diners have good reason to think that the kitchen will not have any soup to serve them, and so cannot reliably visit the kitchen and expect to be served.

This paper provides a method for generating novel concentration inequalities to relate availability and throughput. These concentration inequalities are applicable in a wide variety of domains, and improve upon similar concentration inequalities, such as the Chernoff bound, in ways that are required for a good approximate solution to the soup kitchen problem. Unlike most concentration inequalities, which can only bound the probability that a random variable falls in a region above its mean, the concentration inequalities provided in this paper can bound the probability that a random variable falls in any upward-closed region. In this sense, the concentration inequalities we provide move beyond “tail bounds” and can instead bound a larger class of regions than the tail of a distribution.

A mechanism designer that can fine-tune either the availability or the throughput can use these bounds to establish worst-case values for whichever parameter they do not fine-tune. When demands come from price-sensitive agents, the designer can increase the price to decrease throughput and increase availability, while decreasing the price does the opposite. Furthermore, since the bounds improve as the size of the soup supply κ increases, a designer that increases their supply while targeting a specific availability can increase the value of their worst-case throughput. Alternatively, a designer that increases their supply while targeting a specific throughput can increase the value of their worst-case availability. This allows them to identify the minimal amount of soup κ which permits them to meet their desired values for availability and throughput.

The fact that posted prices can be used to pick a particular point on the tradeoff curve between availability and throughput is particularly useful for prophet inequalities. The conventional way to prove multi-unit prophet inequalities is to demonstrate the existence of a price that achieves a point on the the tradeoff curve which maximizes the posted-price mechanism’s worst-case expected welfare. Better bounds on the worst-case throughput in terms of the availability, or better bounds on the worst-case availability in terms of the throughput, translate into better bounds on expected welfare.

Results

Our primary theorem is a concentration inequality generator. Given a function f that satisfies certain criteria, it constructs a concentration inequality that is either stronger or weaker (and more or less tractable) depending on the function f selected.

Note that, unlike Chernoff bounds, the mean of the demand distribution E[D] does not appear in concentration inequalities generated by Theorem 3. The only quantities relating to the demand D which appear are the availability and the throughput. Furthermore, observe that Theorem 3 permits the selection of thresholds κ which are less than the mean of the demand D, whereas Chernoff bounds do not. Thresholds κ below E[D] permit concentration inequalities generated by Theorem 3 to bound the probability of non-tail regions of the demand D.

To prove Theorem 3, we first establish that the expected value of a convex non-negative function of demand is non-decreasing as we go from general up-to-unit demand to asymmetric unit-demand to binomial (symmetric unit-demand) to Poisson demand (an infinite number of unit demands)[1]. Next we show that the probability of the demand exceeding the threshold κ can be bounded by the expected value of a non-negative convex function f of a binomial distribution with the same expectation as D, normalized by the value of the function on the expected overdemand, i.e. f(E[D | D ≥ κ]). Finally, we show that this bound still holds when all instances of the expected overdemand E[D | D ≥ κ] are lowered to the threshold κ, producing the formula for Theorem 3.

A simple argument then shows that the tightest bound for Theorem 3 comes from a weakly convex function that is zero up to a point and then linear, i.e., f(x) = max(x − β, 0) for some constant β. In machine learning this is referred to as a ReLU function. It is the case that nonReLU bounds, though less tight than ReLU bounds, may still be desirable due to their comparative tractability. We prove several bounds, each produced from a different function f, and compare them to the optimal ReLU bound, showing how different bounds trade off tractability against strength.

Lastly, we apply one of these bounds to the setting of multi-unit prophet inequalities with upto-unit demands. Conventionally, multi-unit prophet inequalities have attempted to showcase the existence of posted prices that produce good expected welfare relative to the optimal allocation, which requires selecting posted prices that sacrifice availability for throughput. The literature on multi-unit prophet inequalities has not explored what occurs when availability is its own independent concern for the mechanism designer, and we show in Theorem 5 that one of the bounds generated by Theorem 3 can be used to illustrate a tractable yet strong bound on the tradeoff between stronger prophet inequalities and availability.

Characterization of Throughput versus Availability

A consequence of the analysis of multi-unit prophet inequalities in Chawla, Devanur, and Lykouris (2023) is a simple (but analytically intractable) characterization of the limits of throughput and availability for unit demands, i.e., when each individual demand Di is in {0, 1}, showing that for any given availability α the worst-case/smallest throughput τ occurs when the total demand D is Poisson-distributed. Therefore, there does not exist any feasible (α, τ ) pairs below the curve drawn out by assuming D is Poisson distributed and varying the Poisson parameter E[D] from E[D] = 0, where (α, τ ) = (1, 0), to E[D] → ∞, where (α, τ ) = (0, 1). Poisson distributions for D with a mean between these two extremes will tradeoff between different intermediate values for throughput and availability.

As mentioned, exact analysis of Poisson tail probabilities are not analytically tractable; that is, given any particular availability, there is no closed form for the corresponding throughput of a Poisson distribution. Our analysis provides concentration inequalities that do give a closed form for worst-case throughput in terms of availability. In addition, our bounds are not restricted to the unit demand setting of multi-unit prophet inequalities. They also hold in a more general setting with up-to-unit demands, i.e. where each Di can take on values in the unit interval [0, 1]. In the setting with up-to-unit demand diners, a simple characterization of the solution to the soup kitchen problem is not known. We conjecture that the worst-case distribution in the up-to-unit-demand setting is also Poisson:

Conjecture. For independently distributed up-to-unit demands with availability and throughput (α, τ ) for a given supply, there is a Poisson distribution for total demand with availability and throughput at most (α, τ ).

Throughout this paper we will use availability-throughput pairs corresponding to Poisson distributions as a benchmark to compare against our concentration inequalities.

Applications

The analysis presented of the soup kitchen problem is applicable in several economic and computational settings.

Consider airline ticket sales, where a clear tradeoff exists between throughput and availability (Bertsimas and De Boer, 2005; Boyd, 2016). Airlines intentionally overbook tickets for seats on a flight knowing that some customers will cancel or not show up (Suzuki, 2002). When more passengers show up than there are seats, an airline must engage in “bumping,” whereby some passengers are removed from the flight, either by way of offering them a voucher for a new flight or rescheduling them for a new one later that day. An airline that tried to set its availability α = 1 will never overbook, but will waste most of the seats on a flight by frequently leaving them empty, exemplified by a low throughput value. Conversely, an airline that aggressively overbooks will achieve a high throughput, but will need to bump passengers so frequently that airline tickets are no longer seen as a reliable indicator for a passenger that they will be boarding a flight at the time printed upon their ticket. Balancing these two quantities is an important tradeoff for the airline to make, and they can control where they fall along the tradeoff curve by changing the degree of overbooking in which they engage.

Analogous tradeoffs occur commonly in cloud computing (Lee and Katz, 2011; Lu et al., 2016) with high fixed cost of compute and storage, and heterogeneity in demand from users. An exemplar is that of major enterprises renting costly GPUs from cloud providers to provision dedicated GPUs to internal users or products (Jeon et al., 2018). Consider a contract where the enterprise rents a fixed supply of GPUs from a provider, and then in turn provisions them out to its employees on demand. Employees’ requests for GPUs arrive in sequence and different requests have different values in terms of productivity for the enterprise. The enterprise would like to maximize its throughput, since it still has to pay for each of the GPUs regardless of whether an employee makes use of them. At the same time, the enterprise also desires high availability. If employees request GPUs and the enterprise consistently cannot fulfil those requests because it has exhausted its supply, it is unproductive for the enterprise. An enterprise can control where it falls on the availability-throughput tradeoff curve by making GPUs easier or harder for employees to acquire. Additionally, rather than trading off between availability and throughput, the enterprise can potentially increase both metrics by increasing the supply of GPUs κ, which improves the entire availability-throughput tradeoff curve. Since it is costly to rent GPUs from a cloud provider, an enterprise may wish to select a minimal supply κ that still permits it to meet its desired availability and throughput values.

Another application arises from designing transaction fee mechanisms for blockchains. A block can accommodate up to κ units of data. The block proposer packs the block with transactions performed by users. Different transactions require different quantities of data (Buterin et al., 2014), and typically the total demand is more than the space available on the block. In the event this occurs, a transaction fee mechanism is deployed to determine which transactions are included in the block. A central question explored in the literature is to design a mechanism that satisfies strategyproofness for users and block proposers, while also deterring collusion between block proposers and users (Roughgarden, 2020; Chung and Shi, 2023). Ethereum, for instance, runs a posted-price mechanism that burns all the payments collected from users (Roughgarden, 2020; Roughgarden, 2021). Whenever the demand at the base price set by the protocol is less than the capacity of the block, the mechanism satisfies all the required properties. On the other hand, when demand exceeds the block capacity, space in the block is allocated through an emergency mechanism, which is a first-price auction in Ethereum’s case. First-price auctions are not strategy-proof for users, while switching to a second-price auction introduces strategic deviations for block proposers. Chung and Shi (2023) show, under some natural assumptions, that there cannot exist a mechanism that guarantees strategy-proofness and collusion resistance for all parties simultaneously. One remedy would be to instead guarantee strategy-proofness and collusion resistance with high probability (cf. Goldberg and Hartline, 2003). High availability corresponds to a lower probability of these periods of over-demand, thereby mitigating the need to run the “undesirable” emergency auction, while a larger throughput corresponds to efficient space utilization in the block (or a lower quantity of information for block proposers to process in the worst-case). The base price can be adjusted to trade off availability (and the strategy-proofness that comes with it) and throughput (and the efficiency that comes with it).

Related Work

Chawla, Devanur, and Lykouris (2023) analyze the same setting and conclude that the worstcase distribution of demand is Poisson, where there are infinitely many agents who all purchase with the same infinitesimally small probability. This result enables numerical calculation of the worst case approximation factor, specifically in the small κ case. Though it is not the main focus of their paper, their analysis that Poisson demand is the worst case for welfare also demonstrates, for our paper, that Poisson demand produces the worst case throughput for any given availability when individuals have unit demands.

Our main theoretical contribution, the development of tail bounds superior to the Chernoff bound, also applies to the special case of individuals with unit demands. This is useful because the tradeoff curve between availability and throughput of the worst-case Poisson demand distribution is not analytically tractable. In contrast, several of the bounds we develop have a closed form.

[1] This last inequality between binomial demand and Poisson demand is eventually used to show that the formula in Theorem 3 is weakest when the number of demands n → ∞.