Authors:
(1) Mehdi Naderi;
(2) Markos Papageorgiou;
(3) Dimitrios Troullinos;
(4) Iasson Karafyllis;
(5) Ioannis Papamichail.
Table of Links
The Nonlinear Feedback Control
OD Corridors and Desired Orientations
Boundary and Safety Controllers
Appendix A: Collision Detection
Appendix B: Transformed ISO-Distance curves
Appendix D: Safety Controller Details
Appendix E: Controller Parameters
IV. OD CORRIDORS AND DESIRED ORIENTATIONS
A. Defining OD Corridors
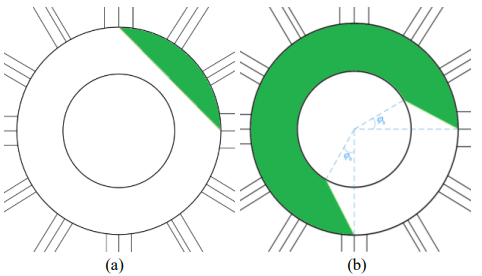
An OD corridor is a part of the roundabout surface, where vehicles with corresponding OD are allowed to drive. In view of the large number of OD couples in big roundabouts, it is sensible to have respective corridors be established automatically, conforming to established rules that come close to human driver decisions. Such corridors can help to mitigate conflicts among vehicles on the roundabout and improve traffic flow. For instance, if a vehicle’s destination is close to its entrance branch, it seems logical to avoid driving close to the inner roundabout boundary, which would expose the vehicle to risky and obstructing quasi-perpendicular movement. The roundabout’s outer boundary is considered as the outer boundary of all OD corridors, as seen in Fig. 5. Conversely, to achieve better infrastructure utilization, a more pertinent definition of the corridors’ interior boundaries is undertaken. First, we categorize ODs into two types: (1) the destination is visible from the origin (Fig. 5(a)); and (2) the destination is not visible from the origin (Fig. 5(b)).
Visible destination: For the first type of OD couples where the origin and destination are relatively close to each other and the destination is visible from the origin, the shortest and simplest way to get there is to take a direct path in the vicinity of or on the outer boundary of the roundabout, avoiding excursions to the inner part of the roundabout. In this sense, a simple choice is to consider a straight line connecting the leftmost point of the origin branch with the left-most point of the destination branch as the inner corridor boundary, see Fig. 5(a). If such a corridor is too narrow for a certain OD, the inner boundary may be replaced by an arc. For the case of Place Charles de Gaulle roundabout, the destination is visible from the origin if it is up to 3 branches away from the origin. If the exit branch is just after the entrance branch, the second option (arc instead of a line) is used for the inner boundary.

B. Specifying Desired Orientations
A vehicle should have some guideline regarding its direction of movement while driving within its OD corridor, so that it first merges in the roundabout traffic, then advances towards its destination and eventually exits. This guideline is provided in the form of desired orientations for the vehicle that are computed based on the vehicle’s current position and its destination and are fed to the NLFC to influence the vehicle movement decisions. Thus, in absence of other vehicles, a vehicle would follow the path imposed by the position-depended desired orientations toward its exit. In the presence of other vehicles, the vehicle may have to deviate from that path, e.g. to avoid collision with other vehicles, but will always have a desired orientation corresponding to its current position.
In this work, we employ a weighted average of two orientations, which are the respective optimal solutions of the shortest path to the destination problem; and the minimum deviation from the circular motion problem, see details in [35]. The shortest path problem: The shortest path connecting any roundabout position with a specific destination has a clear physical meaning; a vehicle would, in absence of other vehicles, have an interest to drive on the shortest path to its destination. Note, however, that such a path may include strong deviations from the circular angle, which, in presence of other vehicles, increase conflicts with rotating vehicles, causing increased delays and collision risk. Shortest-path orientations are readily derived by distinguishing among two cases:

The desired orientation in this part is the slope of the tangent. In the second part, the path follows the inner boundary, i.e., the desired orientation is the circular angle, until the destination gets visible; after which we have again the case of visible destination, and the desired orientation is the slope of a line connected to the exit point, see Fig. 7.

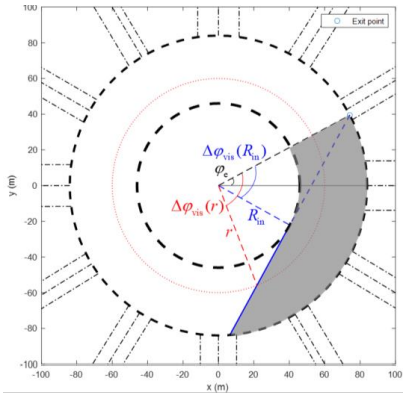
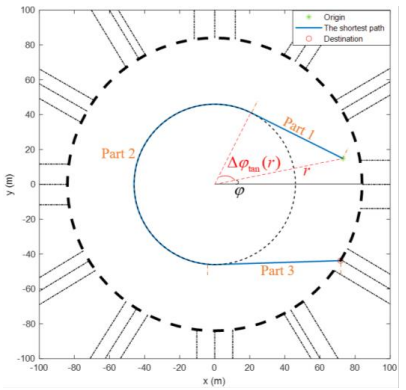
The minimum deviation problem: A path connecting any position in the roundabout with a destination with minimum deviation from circular motion is interesting because most vehicles are rotating and if their orientations are close to the circular angle, then they are close to each other, something that mitigates vehicle conflicts and the strength of any required collision-avoidance maneuvers. In [35], the derived solution of an optimal control problem indicates that deviations from the circular angle are minimized if a vehicle retains a constant deviation on its path from any position to the destination and this constant deviation is

This paper is available on arxiv under CC 4.0 license.

