Table of Links
C. Comparison with Related Works
II. Background
C. Assumptions and Approximations
IV. Results
V. Discussion, Acknowledgments, and References
IV. RESULTS
A. Probability of Success
In this subsection we derive the expression for the quantum miner’s probability of successfully adding a block to the blockchain, or in other words, the expected fractions of blocks they add to the blockchain. Next, we develop a closed-form approximation for this success probability valid in the small computational power regime. Finally, we determine the value of K that optimizes this approximation in the case that the quantum miner is peaceful.
1. Expressions for Transition Probabilities
We begin our determination of success probability by considering the expression for ν. Using Theorem 1, the probability a measurement of a single register Ai at time T yields a marked header is



Finally, we find an expression for the probability φ that if a classical miner finds a block first, the quantum miner also finds a block via aggressive mining. If the quantum miner is following the peaceful protocol, then φ = 0, so here we address the aggressive case. Recall from the analysis of ν that the quantum miner’s measurement after applying k Grover iterations yields a marked header with probability
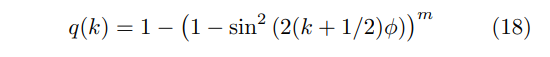
or, using the substitution t := k/r,
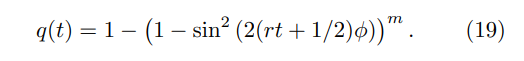

The probability the classical miner finds a block at time t, conditioned on t < T, is
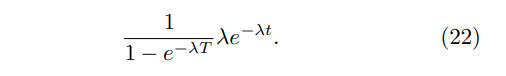
The probability the quantum miner finds an additional block is then
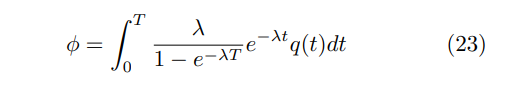
by the law of total probability.

2. Total Probability of Success
Now that we have expressions for the transition probabilities in Figure 1, as well as approximations for these expressions in the √D>>K and K >>1 limit, we analyze the total probability that the quantum miner successfully adds a block to the blockchain. To start, we prove the following lemma
Lemma 1. Starting at state (1), after an infinite number of steps the probability the state is (4) is
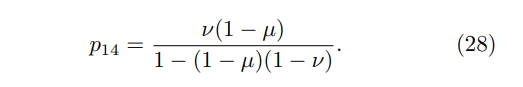
Proof. As the only sequences of states which result in a final state of (4) are (1)(3)(4), (1)(3)(1)(3)(4), (1)(3)(1)(3)(1)(3)(4) and so on, we see that the state (4) can only be reached after an even number of steps. Let w(n) be the probability the state (4) is reached after n steps. Then, the total probability that the final state is (4) is given by
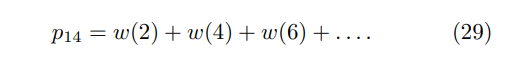
The value of w(n) for n even is
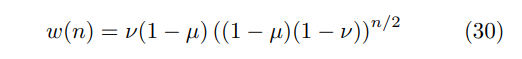
as the only way to arrive at (4) after n steps is to follow the sequence
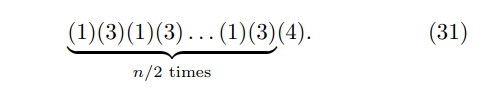
Substituting Eq. 30 into Eq. 29 yields a geometric series:
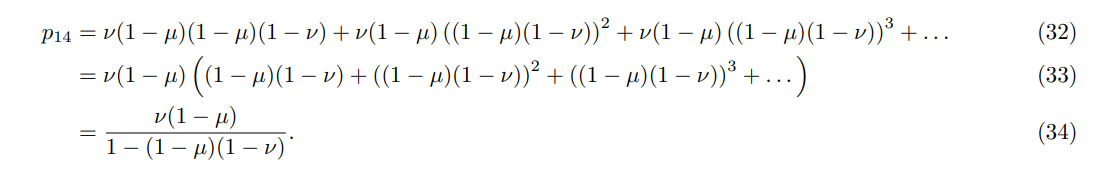

We now derive the total probability that the quantum miner successfully mines a block.
Theorem 2. The probability P := p14 + p18 that the quantum miner successfully adds a block to the blockchain is

Proof. Examination of the state transition graph reveals that the state (2) is visited if and only if the final state (4) is not. Therefore if p12 is the probability that (2) is reached at any number of steps from (1) then
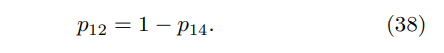
The state transition graph shows that the probability p18 that the final state is (8) is given by
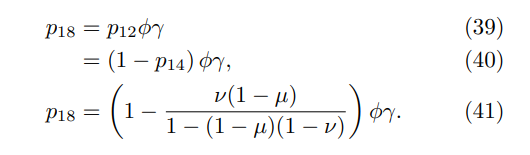
Substituting this expression for p18 into P := p14 + p18 yields the statement of the theorem

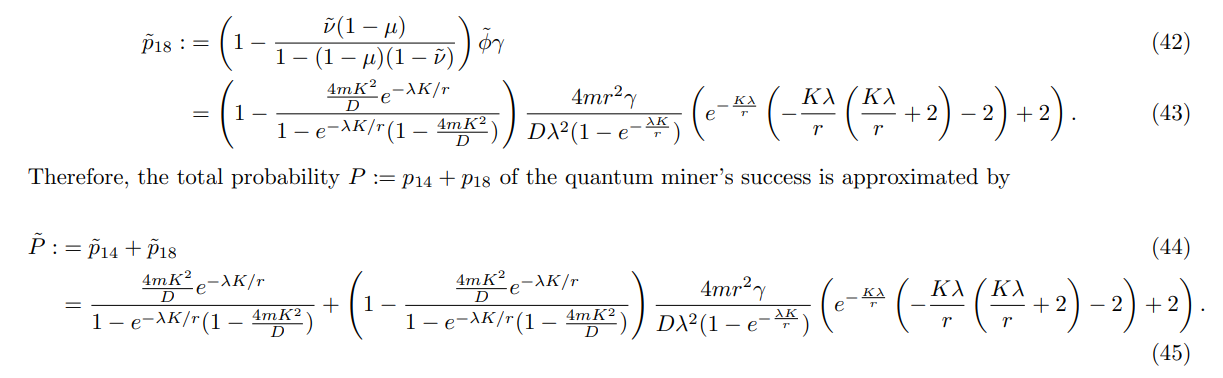
3. Optimal Number of Grover Iterations
Now, we find the value of K which maximizes ˜p14. This value describes the optimal K for quantum mining when γ is small, or when the quantum miner uses only peaceful mining.

Proof. We begin with the variable substitutions
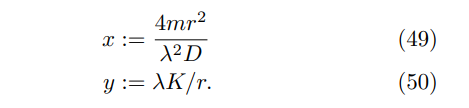
These substitutions yield
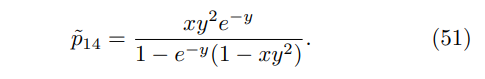
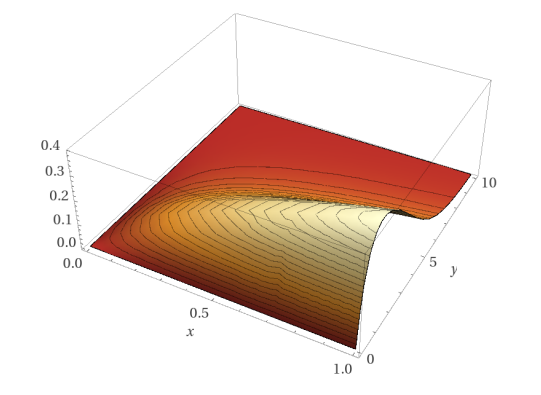
The variable x is a measure of the quantum computers power in relation to problem difficulty. As m, r, λ, D > 0, the value of x is always positive. The variable y determines the time at which the quantum miner should measure, as T = y/λ. Simplifying further,
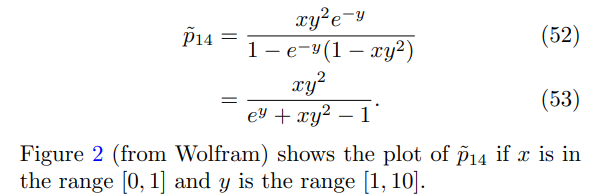
To find the maximum, we take the derivative with respect to y and set this derivative equal to zero:


In other words, if the quantum miner plans to measure at 16 minutes, then there is approximately a 20% chance a classical miner does not find a block before they make this measurement.
Authors:
(1) Robert R. Nerem, Institute for Quantum Science and Technology, University of Calgary, Alberta T2N 1N4, Canada ([email protected]);
(2) Daya R. Gaur, Department of Mathematics and Computer Science, University of Lethbridge, Alberta T1K 3M4, Canada.
This paper is

