Authors:
(1) Davide Viviano, Department of Economics, Harvard University;
(2) Lihua Lei, Graduate School of Business, Stanford University;
(3) Guido Imbens, Graduate School of Business and Department of Economics, Stanford University;
(4) Brian Karrer, FAIR, Meta;
(5) Okke Schrijvers, Meta Central Applied Science;
(6) Liang Shi, Meta Central Applied Science.
Table of Links
Empirical illustration and numerical studies
C Proofs
Throughout the proofs, expectations are conditional on the adjacency matrix A.
C.1 Proof of Lemma 3.1
We have

C.2 Proof of Lemma 3.2

C.3 Proof of Lemma 3.3
We consider the case where two units are in the same or different clusters separately. We will refer to µi(Di , D−i) as µi(D) for notational convenience.


Following the same steps as for the case where i, j are in different clusters, accounting for Equation (27), the proof completes.
C.4 Proof of Lemma 3.4
other units are not zero for individuals in the sets Bi , Gi defined in Lemma 3.2.

where the first inequality is due to Cauchy-Schwarz inequality and last equality follows from Assumption 5. The proof completes after collecting the terms.
C.5 Proof of Theorem 3.5


C.6 Proof of Theorem 3.6

C.7 Proof of Theorem 4.1
The bias follows directly from Lemma 3.1. We now discuss the variance component. Under Lemmas 3.2, 3.3, and following Equations (28), (29), we can write
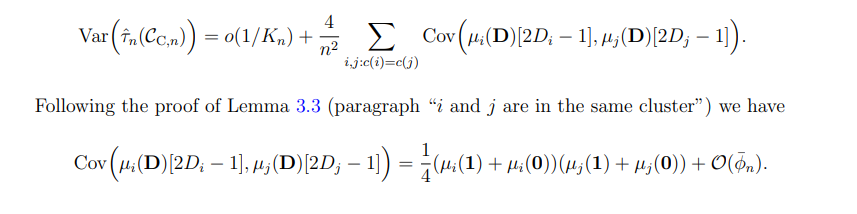

C.8 Proof of Theorem 4.2

C.9 Proof of Theorem 4.3

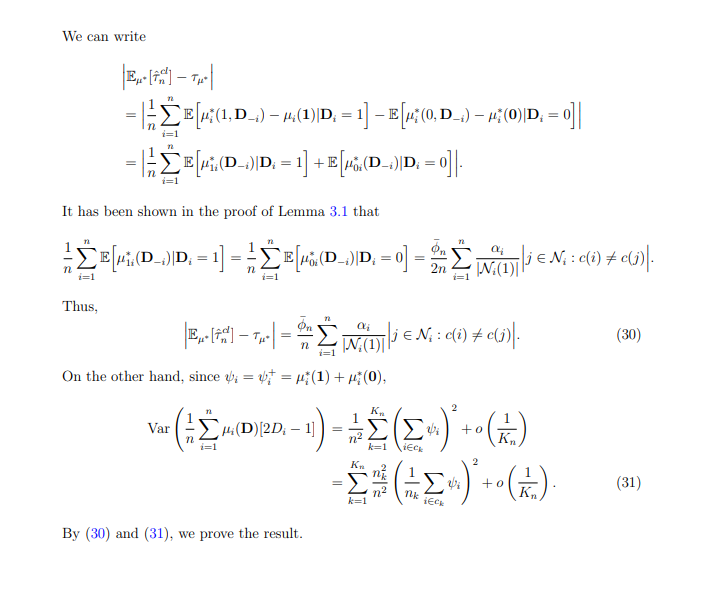
This paper is available on arxiv under CC 1.0 license.

