This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Jihoon Chung;
(2) Zhenyu (James) Kong.
Table of Links
- Abstract & Introduction
- Review of Related Work
- Proposed Research Methodology
- Numerical Case Studies
- Real-World Simulation Case Studies
- Conclusion
- References
III. PROPOSED RESEARCH METHODOLOGY
This section proposes a novel sparse Bayesian hierarchical method: clustering and spatially correlated sparse Bayesian learning (CSSBL). The proposed CSSBL is described in Section III-A, followed by Bayesian inference in Section III-B.
A. Proposed Methodology
The proposed methodology is a sparse Bayesian hierarchical model considering the spatial correlations of KCCs and nonstationarity of process faults along the KPCs samples. From Eq. (2), fault quality linear model of k th KPCs sample (yk ) can be written as follows:

The prior distributions in the proposed method consist of the following two hierarchical layers. The first layer provides several prior distributions. First, the prior distribution of precision variable α in Eq. (4) is provided. Second, the prior distribution exploiting the spatial correlation of KCCs is offered. Finally, the prior distribution in the first layer clusters the KPCS samples into groups
sharing the same process faults. The second layer consists of prior distribution encouraging the sparsity of process faults. Fig. 2 describes a graphical representation of the hierarchical layers in the proposed method.
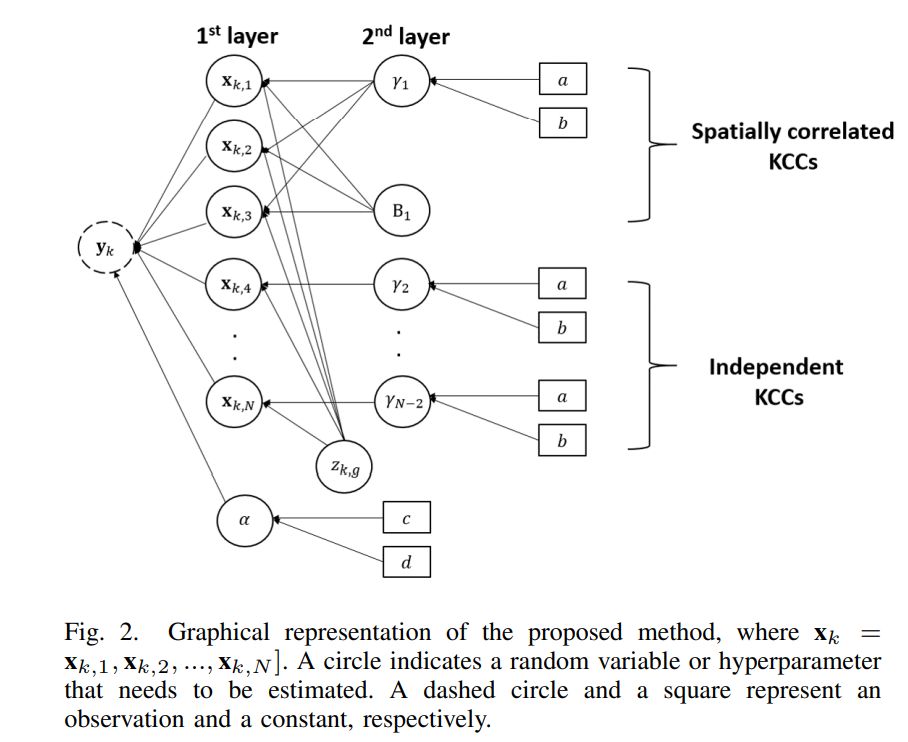
In the first layer of the hierarchical model in Fig. 2, the Gamma distribution is provided as the prior distribution of α in Eq. (4) as follows:

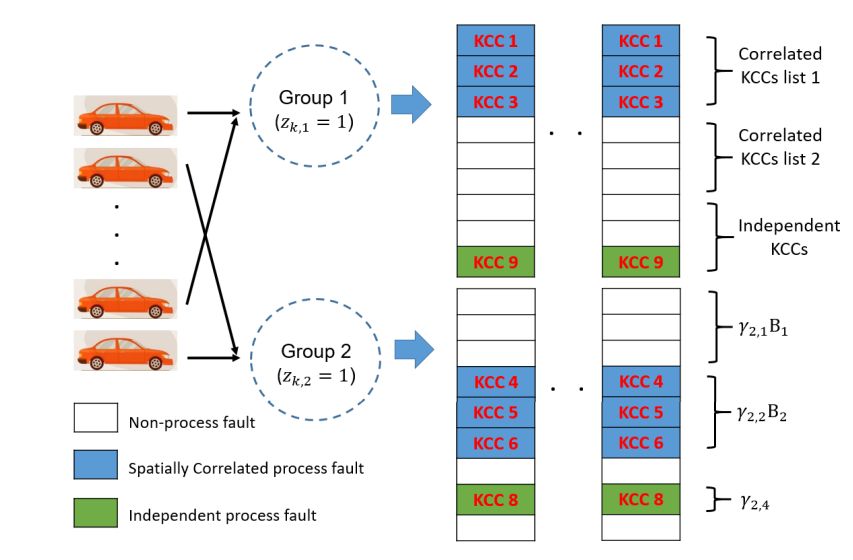
To handle the spatial correlation of KCCs, the proposed approach considers two types of correlation structures of fixture locators in multistation assembly systems. One is an independent locator whose deviation is uncorrelated to the deviation of other locators (i.e., independent tolerance mode in [21]). The other is correlated locators (i.e., composite tolerance mode in [21]). Specifically, the locators in the correlated list vary with a certain correlation with other locators in the list [21]. To consider this structure, the proposed method models the covariance matrix (Ck) of the prior distribution of xk in Eq. (5) as follows:



B. Bayesian Inference of the Proposed Methodology

To address this challenge, this paper employs Variational Bayes inference (VBI) to derive approximate posterior distributions of hidden variables. Specifically, Variational Bayes Expectation Maximization (VBEM) [41] estimates hidden variables and hyperparameters to identify KCCs with excessive variance in the proposed method. VBEM consists of Estep: Variational Bayesian expectation step to estimate hidden variables X, Z, Γ, α by approximating the posterior distribution of hidden variables; and M-step: Variational Bayesian maximization step to update hyperparameters B by maximizing the expected value of the logarithm of the complete likelihood [37].







