This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Mattia Atzeni, EPFL, Switzerland and [email protected];
(2) Mrinmaya Sachan, ETH Zurich, Switzerland;
(3) Andreas Loukas, Prescient Design, Switzerland.
Table of Links
- Abstract & Introduction
- Formalizing the Group-Action Learning Problem
- Attention Masks for Core Geometry Priors
- The LATFORMER Architecture
- Experiments
- Related Work
- Conclusion & References
- A. Additional Details on the Model
- B. Additional Experiments and Details on the Experimental Setup
- C. Limitations and Future Work
- D. Deferred Proofs
A. Additional Details on the Model
This section describes the LATFORMER architecture providing additional details that were not covered in Section 4.1. As mentioned in Section 4.1, it is possible to design convolutional neural networks that perform all considered transformations of the lattice. Figure 6 shows the architecture of the four expert models that generate translation, rotation, reflection and scaling masks.
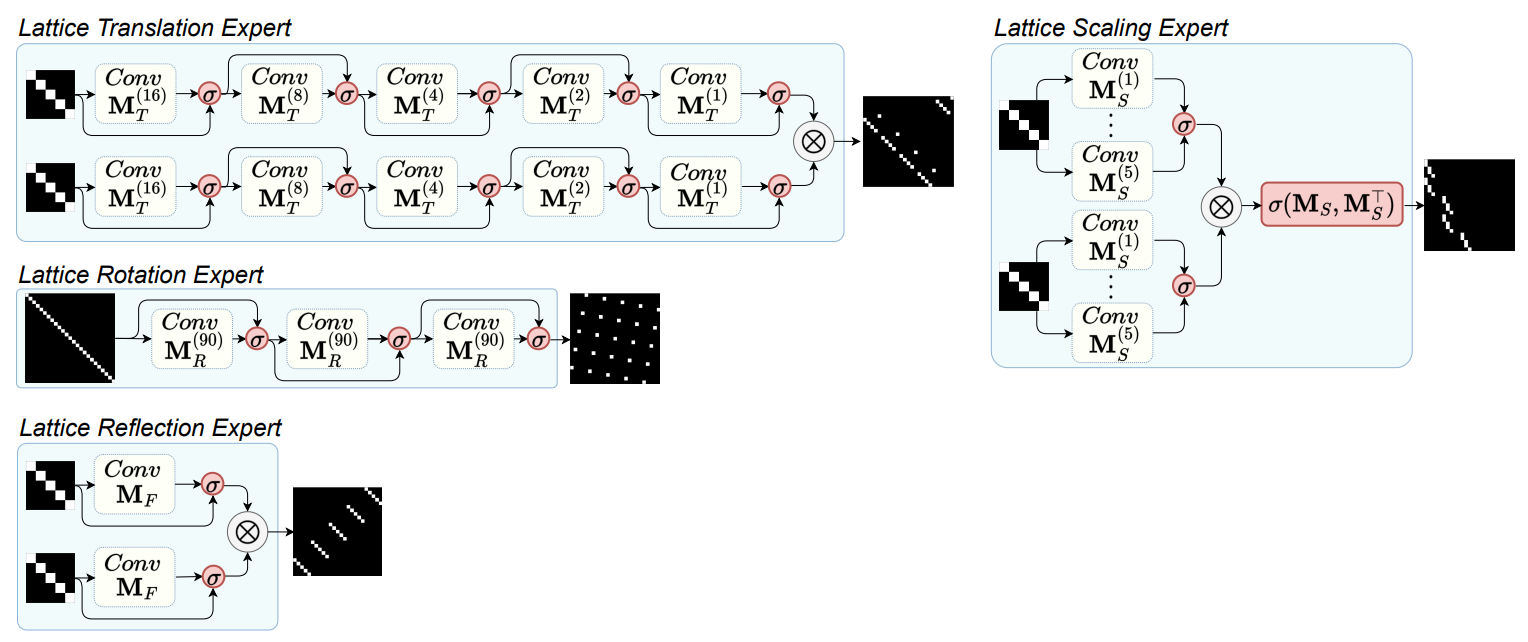
All models are CNNs applied to the identity matrix. In the figure, we use the following notation:
• M(δ) T denotes an attention mask implementing a translation by δ along one dimension;
• M(90) R denotes an attention mask implementing a translation by 90◦ ;
• MF denotes an attention mask implementing a reflection along one dimension;
• M(h) S denotes an attention mask implementing an upscaling by h along one dimension.
Using Corollary 3.3, we can derive the kernels of the convolutional layers shown in Figure 6. These kernels are frozen at training time, the model only learns the gating function, denoted as σ in the figure. Notice that all the models follow the same overall structure. However, for scaling, we also learn an additional gate, denoted as σ(MS,M⊤ S ) in the Figure 6. This gate allows the model to transpose the mask and serves the purpose of implementing down-scaling operations (down-scaling is the transpose of up-scaling).
The composition of more actions can be obtained by combining different experts. This can be done either by chaining the experts or by matrix multiplication of the masks. In preliminary experiments, we did not notice any significant difference in performance between the two options and we rely on the latter in our implementation.

