This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Mattia Atzeni, EPFL, Switzerland and [email protected];
(2) Mrinmaya Sachan, ETH Zurich, Switzerland;
(3) Andreas Loukas, Prescient Design, Switzerland.
Table of Links
- Abstract & Introduction
- Formalizing the Group-Action Learning Problem
- Attention Masks for Core Geometry Priors
- The LATFORMER Architecture
- Experiments
- Related Work
- Conclusion & References
- A. Additional Details on the Model
- B. Additional Experiments and Details on the Experimental Setup
- C. Limitations and Future Work
- D. Deferred Proofs
5. Experiments
To evaluate our method, we first developed a set of synthetic tasks in order to compare LATFORMER to attention modules and Transformers with respect to sample efficiency in learning basic geometric transformations. Then, we annotated the ARC tasks based on the knowledge priors they require, and we assessed the performance of our method on this challenging dataset. Finally, we experimented with the LARC (Acquaviva et al., 2021) dataset and compared our method to stronger baselines based on neural program synthesis. We report additional experimental results in Appendix B.5.
5.1. Sample Efficiency on Geometric Transformations
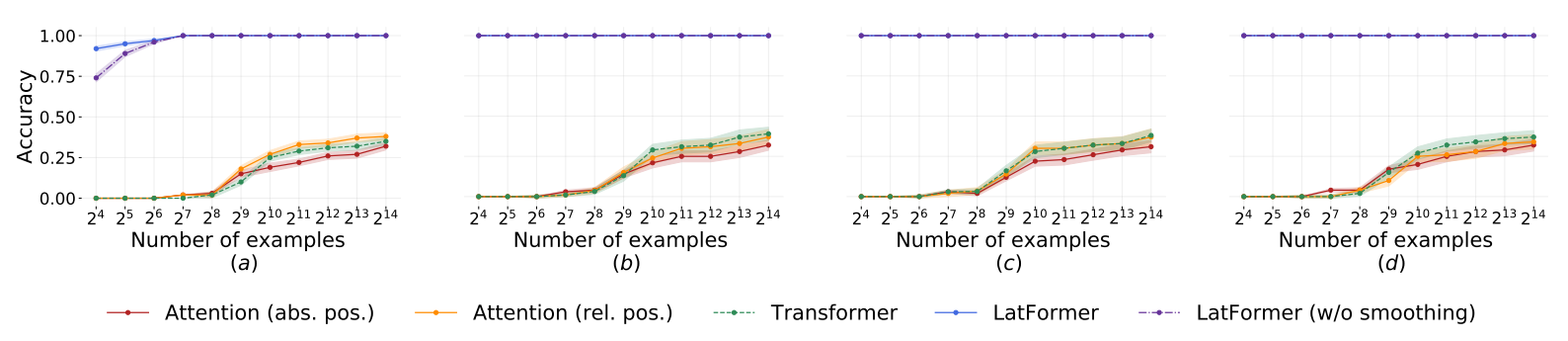
As a preliminary study, we probed the ability of LATFORMER to learn geometric transformations efficiently. To this end, we compared the performance of our model to a transformer (Vaswani et al., 2017) and an attention module (the same architecture as our approach, without the mask expert) on synthetic tasks with increasing number of examples. Inspired by ARC, we generated a set tasks where the model needs to infer a geometric transformation from input-output pairs. The input is a grid taken from the ARC tasks and the output is either a translation, rotation, reflection or scaling of the input. The specific transformation applied to the input grid defines the task and is consistent across all examples in the same task.
We evaluated the models based on the mean accuracy across tasks. Figure 5 shows the accuracy of our model compared to the baselines and to a version of LATFORMER without smoothing. The plots show that LATFORMER can generalize better and from fewer examples than transformers and attention modules both with absolute positional encodings (Vaswani et al., 2017) and relative positional encodings (Shaw et al., 2018). Additionally, our results show that the smoothing operation described in Section 4.2 is helpful for larger groups. More details on this experiment are reported in Appendix B.1.
5.2. Geometric Reasoning on ARC Tasks
To assess the ability of our approach to learn efficiently on a more challenging use case, we focused on a subset of the ARC dataset (Chollet, 2019) requiring geometric priors for which our method could be a principled solution. To this end, we annotated the ARC tasks based on the knowledge priors they require, using the list of priors provided by Chollet (2019) as a reference. Appendix B.2 provides more details about the annotation of ARC and Figure 7a in the Appendix shows the knowledge priors that we considered and their distribution across the ARC tasks.
We assessed the performance of our model on the tasks that require only knowledge priors corresponding to the basic geometrical transformations that we addressed in this work, namely translation, rotation, reflection and scaling. Table 2 shows our results compared to neural baselines, including CNNs, attention with relative positional encodings (Shaw et al., 2018), PixelCNN (Gul et al., 2019), and Transformers (Vaswani et al., 2017), and a Differentiable Neural Computer (Graves et al., 2016) with spectral regularization (Kolev et al., 2020). We additionally compared to a Transformer model that has access to precomputed transformations of the input (Transformer + data augmentation). Precomputing all group actions is only feasible for smaller groups (rotation, reflection and scaling).
Further, Table 2 reports the performance obtained by a search algorithm applied on top of a hand-engineered domain-specific language (DSL). This approach searches all possible programs in the DSL that can map the input grids to the corresponding output grids successfully. We use the implementation of Wind (2020), which obtained the best results at the ARC Kaggle competition out of almost 1000 submissions 3 . This approach does not use any learnable component and the results are provided as a reference. We notice that LATFORMER significantly reduces the gap between neural networks and the current best approach for ARC, even outperforming the search algorithm for one category of tasks.
Though we restrict to only a subset of the tasks and there is definitely room for improvement even on these tasks, we reach considerably better performance than the baselines. Therefore, we believe our results advocate for the applicability of end-to-end differentiable models even on problems requiring sample-efficient abstract reasoning. To the extent of our knowledge, this is the first evidence of a neural network achieving this performance on ARC tasks.
5.3. Comparison with Neural Program Synthesis
Recently, Acquaviva et al. (2021) introduced the Languagecomplete Abstraction and Reasoning Corpus (LARC), which provides natural language descriptions of 88% of the ARC tasks, generated by human participants who where asked to communicate to other humans a set of precise instructions to solve a task.
Acquaviva et al. (2021) evaluated several models based on neural program synthesis on LARC. All models generate symbolic programs from a carefully designed domainspecific language (DSL) following a generate-and-check strategy. First a neural model generates a program from the grammar of the DSL (Ellis et al., 2020) and then the program is checked against the input-output pairs to ensure that it can generate all training examples.
We compare against the following baselines identified by Acquaviva et al. (2021). LARC (IO) is a model that has only access to input-output pairs, as our LATFORMER. LARC (IO + NL) has access to the natural language descriptions as well and uses a pre-trained T5 model (Raffel et al., 2020) to represent the text. LARC (IO + NL pseudo) uses pseudoannotation to encourage the learning of compositional relationships between language and programs: during training, the model is given additional synthetic language-to-program pairs generated by annotating primitive examples in the DSL with linguistic comments. We refer the reader to Appendix B.3 for more details.
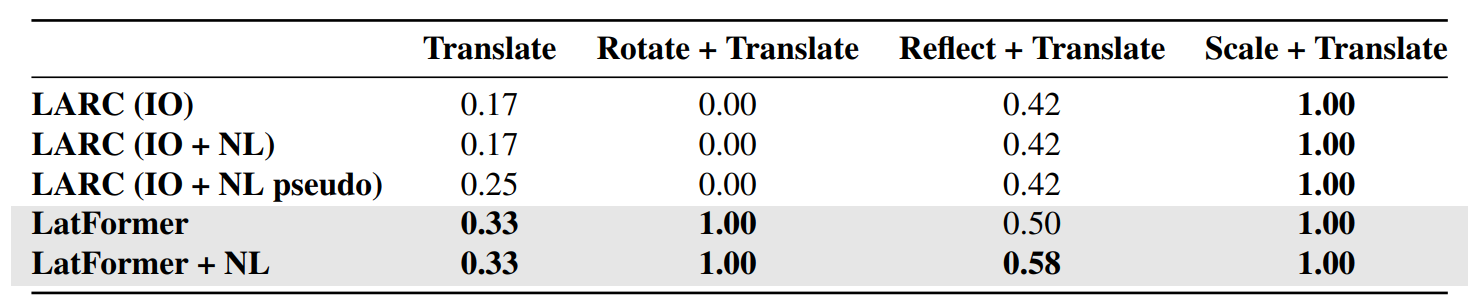
In order to compare to the work of Acquaviva et al. (2021), we evaluated their models on the set of LARC tasks that correspond to ARC tasks in our subset requiring geometric knowledge priors. Additionally, following Acquaviva et al. (2021) we allowed LATFORMER to access the textual descriptions by using a pre-trained T5 model to generate a representation of the text. This embedding is provided as input both to the Lattice Mask Expert and the FFN layers of LATFORMER (LatFormer + NL). Table 3 shows the results of our experiments on the LARC dataset. The programsynthesis methods require a training stage on a portion of the tasks. Therefore, the LATFORMER models where only evaluated on the same testing tasks of LARC, using the same train-test split of Acquaviva et al. (2021). Overall, our results show that LATFORMER performs better than program synthesis on the subset of tasks requiring geometric priors, with no need for a carefully designed DSL. This advantage comes to the expense of being restricted to tasks involving geometric priors, whereas program-synthesis approaches can be used on a wider set of tasks. We also observe that the natural language descriptions marginally helped our model on one category of tasks. Our findings corroborate with Acquaviva et al. (2021) in this remark.
Table 2: Performance on ARC tasks that involve lattice symmetry priors.
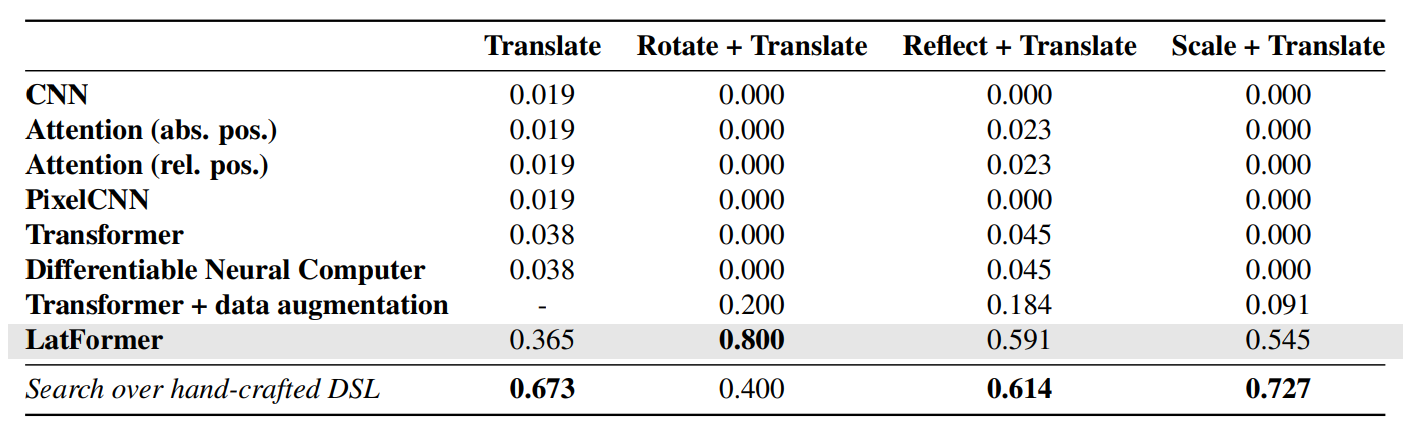
Table 3: Comparison of LATFORMER with neural program synthesis methods with access to both input-output pairs and natural language descriptions on LARC