The Economics of Being Fashionably Late to the Auction Party

Table of Links

Abstract

1. Introduction

   1.1 Periodic auction and continuous limit order book

   1.2 Comparison and main flaws of limit order book

   1.3 Optimal policies to cure auction’s inefficiencies and related works

2. Auctions market modeling with transaction fees and randomization

   2.1 The market characteristics

   2.2 Clearing Price rule

   2.3 Strategic Trader’s optimization and market quality

   2.4 Data and numerical analysis

   2.5 Strategic trader with full information: efficient but unfair market

   2.6 Imperfect information and inefficiency of auctions

3. Monitoring policies: transaction fees and clearing time randomization

   3.1 Bilevel optimization between the exchange and the strategic trader

   3.2 Randomization without fees

   3.3 Optimal transaction fees indexed on time to improve price impact for the trader

   3.4 Optimal transaction fees indexed on time: improving market quality while benefiting from the fees

4. Conclusions

A. Appendix: Numerical Methods

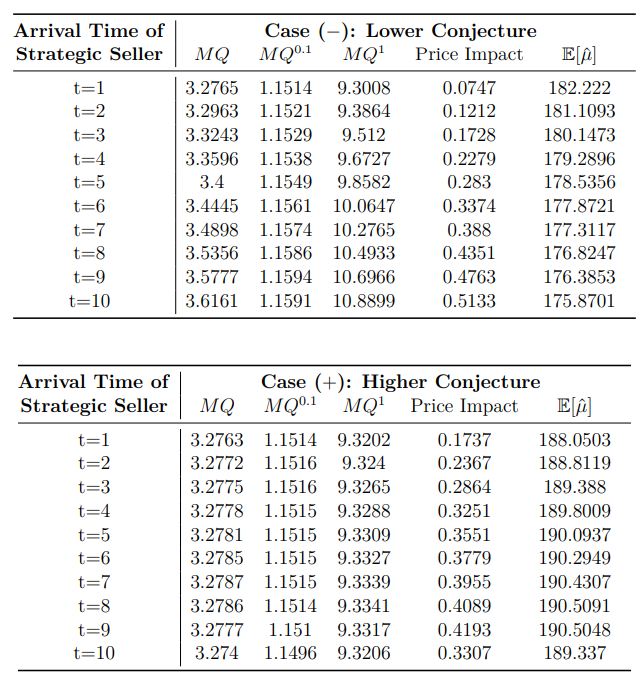
A.1 Problem of a Strategic Seller

A.2 Appendix: Problem of the Regulator

B Appendix: Illustrate Remark 2.4

References

2.3 Strategic Trader’s optimization and market quality

2.3.1 Strategic trader optimization

Since the strategic seller wants to maximize payoff, the seller’s problem is written as:

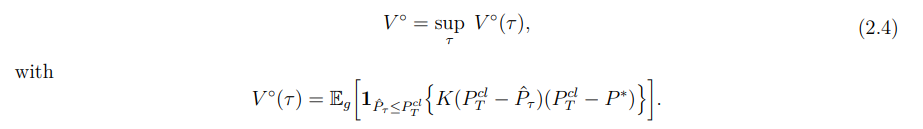
Intuitively, the optimal arrival of the trader should be always T as the trader could use more information to make decisions. The following theorem proves that the optimal time to arrive is indeed τ = T; the later the trader joins the auction the better the payoff.

2.3.2 Market quality and exchange’s viewpoint

We introduce two different measures (disutility functions) of market quality:

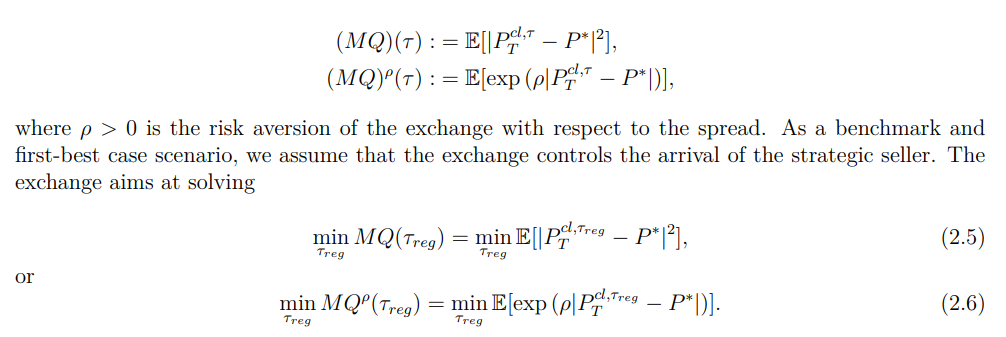
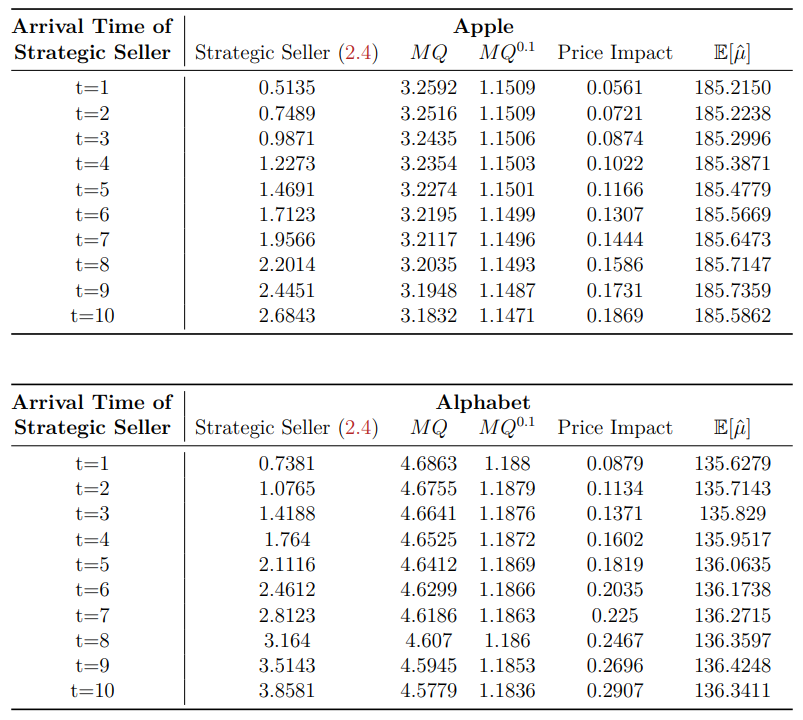
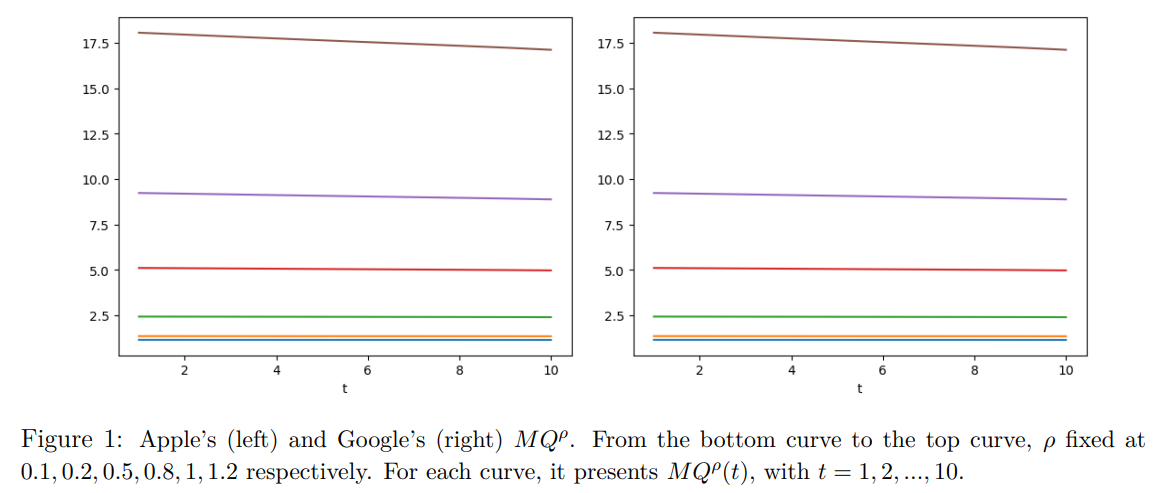
2.4 Data and numerical analysis

We assume that the slope of the supply function is K = 10 and take λ = 1 in consideration of the computation cost.

2.5 Strategic trader with full information: efficient but unfair market

Theorem 2. Assume that the strategic trader is either a seller or a buyer, i.e., the trader’s objective is defined as

The function f defined by

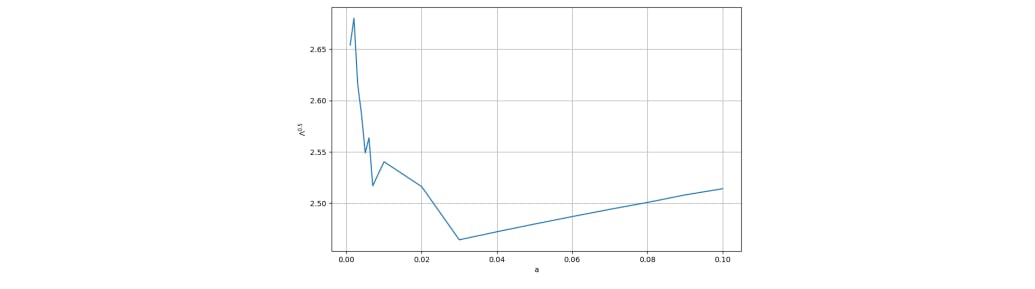
2.5.2 Numerical results and economical insights

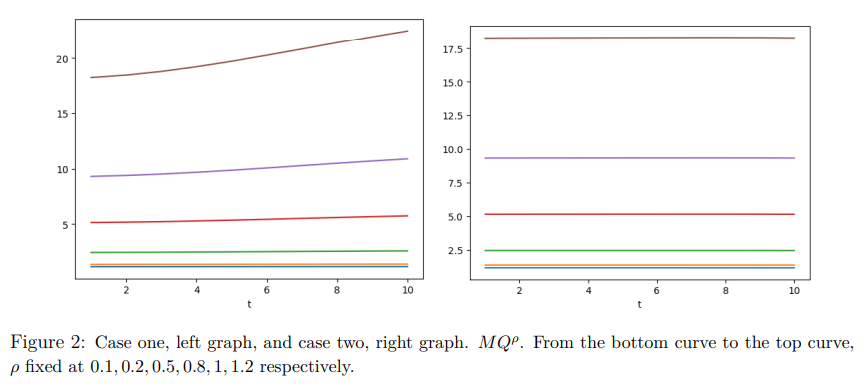
2.6 Imperfect information and inefficiency of auctions