This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Ruta Jawale;
(2) Dakshita Khurana.
Table of Links
Unclonable Non-Interactive Zero-Knowledge in the CRS Model
Unclonable NIZK in the Quantum Ramdon Oracle Model
Unclonable Signatures of Knowledge
Abstract
A non-interactive ZK (NIZK) proof enables verification of NP statements without revealing secrets about them. However, an adversary that obtains a NIZK proof may be able to clone this proof and distribute arbitrarily many copies of it to various entities: this is inevitable for any proof that takes the form of a classical string. In this paper, we ask whether it is possible to rely on quantum information in order to build NIZK proof systems that are impossible to clone.
We define and construct unclonable non-interactive zero-knowledge proofs (of knowledge) for NP. Besides satisfying the zero-knowledge and proof of knowledge properties, these proofs additionally satisfy unclonability. Very roughly, this ensures that no adversary can split an honestly generated proof of membership of an instance x in an NP language L and distribute copies to multiple entities that all obtain accepting proofs of membership of x in L. Our result has applications to unclonable signatures of knowledge, which we define and construct in this work; these non-interactively prevent replay attacks.
1 Introduction
Zero-knowledge (ZK) [GMR89] proofs allow a prover to convince a verifier about the truth of an (NP) statement, without revealing secrets about it. These are among the most widely used cryptographic primitives, with a rich history of study.
Enhancing Zero-knowledge. ZK proofs for NP are typically defined via the simulation paradigm. A simulator is a polynomial-time algorithm that mimics the interaction of an adversarial verifier with an honest prover, given only the statement, i.e., x ∈ L, for an instance x of an NP language L. A protocol satisfies zero-knowledge if it admits a simulator that generates a view for the verifier, which is indistinguishable from the real view generated by an honest prover. This captures the intuition that any information obtained by a verifier upon observing an honestly generated proof, could have been generated by the verifier “on its own” by running the simulator.
Despite being widely useful and popular, there are desirable properties of proof systems that (standard) simulation-based security does not capture. For example, consider (distributions over) instances x of an NP language L where it is hard to find an NP witness w corresponding to a given instance x. In an “ideal” world, given just the description of one such NP statement x ∈ L, it is difficult for an adversary to find an NP witness w, and therefore to output any proofs of membership of x ∈ L. And yet, upon obtaining a single proof of membership of x ∈ L, it may suddenly become feasible for an adversary to make many copies of this proof, thereby generating several correct proofs of membership of x ∈ L.
Unfortunately, this attack is inevitable for classical non-interactive proofs: given any proof string, an adversary can always make multiple copies of it. And yet, there is hope to prevent such an attack quantumly, by relying on the no-cloning principle.
Indeed, a recent series of exciting works have combined cryptography with the no-cloning principle to develop quantum money [Wie83, AC13, FGH+12, Zha19a, Kan18], quantum tokens for digital signatures [BS16], quantum copy-protection [Aar09, AP21, ALL+21, CLLZ21], unclonable encryption [Got03, BL20, AK21, MST21, AKL+22], unclonable decryption [GZ20], one-outof-many unclonable security [KN23], and more. In this work, we combine zero-knowledge and unclonability to address a question first posed by Aaronson [Aar09]:
Can we construct unclonable quantum proofs?
How do these proofs relate to quantum money or copy-protection?
1.1 Our Results
We define and construct unclonable non-interactive zero-knowledge proofs of knowledge (NIZKPoK). We obtain a construction in the common reference string (CRS) model, as well as one in the quantum(-accessible) random oracle model (QROM). The CRS model allows a trusted third-party to set up a structured string that is provided to both the prover and verifier. On the other hand, the QROM allows both parties quantum access to a truly random function O.
In what follows, we describe our contributions in more detail.
1.1.1 Definitional Contributions
Before discussing how we formalize the concept of unclonability for NIZKs, it will be helpful to define hard distributions over NP instance-witness pairs.
Hard Distributions over Instance-Witness Pairs. Informally, an efficiently samplable distribution over instance-witness pairs of a language L is a “hard” distribution if given an instance sampled randomly from this distribution, it is hard to find a witness. Then, unclonable security requires that no adversary given an instance x sampled randomly from the distribution, together with an honestly generated proof, can output two accepting proofs of membership of x ∈ L.
More specifically, a hard distribution (X ,W) over RL satisfies the following: for any polynomialsized (quantum) circuit family {Cλ}λ∈N,
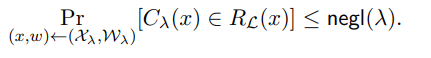
For the sake of simplifying our subsequent discussions and definitions, let us fix a NP language L with corresponding relation R. Let (X ,W) be some hard distribution over R.
A Weaker Definition: Unclonable Security. For NIZKs satisfying standard completeness, soundness and ZK, we define a simple, natural variant of unclonable security as follows. Informally, a proof system satisfies unclonable security if, given an honest proof for an instance and witness pair (x, w) sampled from a hard distribution (X ,W), no adversary can produce two proofs that verify with respect to x except with negligible probability.
Definition 1.1. (Unclonable Security of NIZK). A NIZK proof (Setup, Prove,Verify) satisfies unclonable security if for every language L and every hard distribution (X ,W) over RL, for every poly-sized circuit family {Cλ}λ∈N,

In the definition above, we aim to capture the intuition that one of the two proofs output by the adversary can be the honest proof they received, but the adversary cannot output any other correct proof for the same statement. Of course, such a proof is easy to generate if the adversary is able to find the witness w for x, which is exactly why we require hardness of the distribution (X ,W) to make the definition non-trivial.
We also remark that unclonable security of proofs necessitates that the proof π keep hidden any witnesses w certifying membership of x in L, as otherwise an adversary can always clone the proof π by generating (from scratch) another proof for x given the witness w.
A Stronger Definition: Unclonable Extractability. We can further strengthen the definition above to require that any adversary generating two (or more) accepting proofs of membership of x ∈ L given a single proof, must have generated one of the two proofs “from scratch” and must therefore “know” a valid witness w for x. This will remove the need to refer to hard languages.
In more detail, we will say that a proof system satisfies unclonable extractability if, from any adversary A that on input a single proof of membership of x ∈ L outputs two proofs for x, then we can extract a valid witness w from A for at least one of these statements with high probability. Our (still, simplified) definition of unclonable extractability is as follows.
Definition 1.2 (Unclonable Extractability.). A proof (Setup, Prove,Verify) satisfies unclonable security there exists a QPT extractor E which is an oracle-aided circuit such that for every language L with corresponding relation RL and for every non-uniform polynomial-time quantum adversary A, for every instance-witness pair (x, w) ∈ RL and λ = λ(|x|), such that there is a polynomial p(·) satisfying:
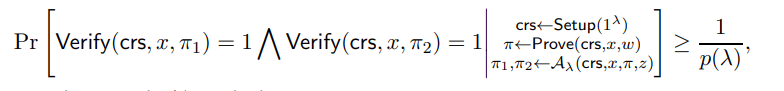
there is also a polynomial q(·) such that
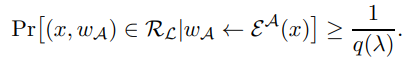
In fact, in the technical sections, we further generalize this definition to consider a setting where the adversary obtains an even larger number (say k−1) input proofs on instances x1, . . . , xk−1, and outputs k or more proofs. Then we require the extraction of an NP witness corresponding to any proofs that attempt to “clone” honestly generated proofs (i.e. the adversary outputs two or more proofs w.r.t. the same instance xi ∈ {x1, . . . , xk−1}). All our theorem statements hold w.r.t. this general definition. Finally, we also consider definitions and constructions in the quantum-accessible random oracle model (QROM); these are natural generalizations of the definitions above, so we do not discuss them here.
We also show that the latter definition of unclonable extractability implies the former, i.e. unclonable security. Informally, this follows because the extractor guaranteed by the definition of extractability is able to obtain a witness w for x from any adversary, which contradicts hardness of the distribution (X ,W). We refer the reader to Appendix A for a formal proof of this claim.
1.1.2 Realizations of Unclonable NIZK, and Relationship with Quantum Money
We obtain realizations of unclonable NIZKs in both the common reference string (CRS) and the quantum random oracle (QRO) models, assuming public-key quantum money mini-scheme and other (post-quantum) standard assumptions. We summarize these results below.
Theorem 1.3 (Informal). Assuming public-key quantum money mini-scheme, public-key encryption, perfectly binding and computationally hiding commitments, and adaptively sound NIZK proofs for NP, there exists an unclonable NIZKPoK scheme in the CRS model.
Theorem 1.4 (Informal). Assuming public-key quantum money mini-scheme and honest verifier zeroknowledge proofs of knowledge (HVZKPoKs) for NP, there exists an unclonable NIZKPoK scheme in the QROM.
Theorem 1.5 (Informal). Assuming public-key quantum money mini-scheme, public-key encryption, postquantum perfectly binding and computationally hiding commitments, and simulation-sound NIZK proofs for NP, there exists an unclonable signature of knowledge in the CRS model.
Is Quantum Money necessary for Unclonable NIZKs? Our work builds unclonable NIZKs for NP by relying on any (public-key) quantum money scheme (mini-scheme), in conjuction with other assumptions such as NIZKs for NP. Since constructions of public-key quantum money minischeme are only known based on post-quantum indistinguishability obfuscation [AC13, Zha19b], it is natural to wonder whether the reliance on quantum money is inherent. We show that this is indeed the case, by proving that unclonable NIZKs in fact imply public-key quantum money mini-scheme.
Theorem 1.6 (Informal). Unclonable NIZKs for NP imply public-key quantum money mini-scheme.
1.1.3 Applications
Unclonable Signatures of Knowledge. A (classical) signature scheme asserts that a message m has been signed on behalf of a public key pk. However, in order for this signature to be authenticated, the public key pk must be proven trustworthy through a certification chain rooted at a trusted public key PK. However, as [CL06] argue, this reveals too much information; it should be sufficient for the recipient to only know that there exists a public key pk with a chain of trust from PK. To solve this problem, [CL06] propose signatures of knowledge which allow a signer to sign on behalf of an instance x of an NP-hard language without revealing its corresponding witness w. Such signatures provide an anonymity guarantee by hiding the pk of the sender.
While this is ideal for many applications, anonymity presents the following downside: a receiver cannot determine whether they were the intended recipient of this signature. In particular, anonymous signatures are more susceptible to replay attacks. Replay attacks are a form of passive attack whereby an adversary observes a signature and retains a copy. The adversary then leverages this signature, either at a later point in time or to a different party, to impersonate the original signer. The privacy and financial consequences of replay attacks are steep. They can lead to data breach attacks which cost millions of dollars annually and world-wide [IBM23].
In this work, we construct a signature of knowledge scheme which is the first non-interactive signature in the CRS model that is naturally secure against replay attacks. Non-interactive, replay attack secure signatures have seen a lot of recent interest including a line of works in the bounded quantum storage model [BS23b] and the quantum random oracle model [BS23a]. Our construction is in the CRS model and relies on the hardness of NP problems, plausible cryptographic assumptions, and the axioms of quantum mechanics. We accomplish this by defining unclonable signatures of knowledge: if an adversary, given a signature of a message m with respect to an instance x, can produce two signatures for m which verify with respect to the same instance x, then our extractor is able to extract a witness for x.
Our construction involves showing that an existing compiler can be augmented using unclonable NIZKs to construct unclonable signatures of knowledge. The authors of [CL06] construct signatures of knowledge from CPA secure dense cryptosystems [SP92, SCP00] and simulationsound NIZKs for NP [Sah99, SCO+01]. Signatures of knowledge are signature schemes in the CRS model for which we associate an instance x in a language L. This signature is simulatable, so there exists a simulator which can create valid signatures without knowledge of a witness for x. Additionally, the signature is extractable which means there is an extractor which is given a trapdoor for the CRS and a signature, and is able to produce a witness for x. We show that, by switching the simulation-sound NIZKs for unclonable simulation-extractable NIZKs (and slightly modifying the compiler), we can construct unclonable signatures of knowledge.
Relationship with Revocation. A recent exciting line of work obtains certified deletion for time-lock puzzles [Unr14], non-local games [FM18], information-theoretic proofs of deletion with partial security [CW19], encryption schemes [BI20, BK23], device-independent security of one-time pad encryption with certified deletion [KT20], public-key encryption with certified deletion [HMNY21], commitments and zero-knowledge with certified everlasting hiding [HMNY22], and fully-homomorphic encryption with certified deletion [Por22, BK23, BKP23, BGG+23]. While certified everlasting deletion of secrets has been explored in the context of interactive zero-knowledge proofs [HMNY22], there are no existing proposals for non-interactive ZK satisfying variants of certified deletion. Our work provides a pathway to building such proofs.
In this work, we construct a quantum revocable anonymous credentials protocol by way of the hardness of NP problems, plausible cryptographic assumptions, and the axioms of quantum mechanics. Our work follows a line of work on (classical) revocation for anonymous credentials schemes [BCC+09, CKS10, AN11].
In particular, our construction involves noting that NIZK proof systems that are unclonable can also be viewed as supporting a form of certified deletion/revocation, where in order to delete, an adversary must simply return the entire proof. In other words, the (quantum) certificate of deletion is the proof itself, and this certificate can be verified by running the NIZK verification procedure on the proof. The unclonability guarantee implies that an adversary cannot keep with itself or later have the ability to generate another proof for the same instance x. In the other direction, in order to offer certifiable deletion, a NIZK must necessarily be unclonable. To see why, note that if there was an adversary who could clone the NIZK, we could use this adversary to obtain two copies, and provably delete one of them. Even though the challenger for the certifiable deletion game would be convinced that its proof was deleted, we would still be left with another correct proof.
1.2 Related Works
This work was built upon the foundations of and novel concepts introduced by prior literature. We will briefly touch upon some notable such results in this section.
Unclonable Encryptions. Unclonable encryption [Got03, BL20, AK21, MST21, AKL+22] imagines an interaction between three parties in which one party receives a quantum ciphertext and splits this ciphertext in some manner between the two remaining parties. At some later point, the key of the encryption scheme is revealed, yet both parties should not be able to simultaneouly recover the underlying message. While our proof systems share the ideology of unclonability, we do not have a similar game-based definition of security. This is mainly due to proof systems offering more structure which can take advantage of to express unclonability in terms of simulators and extractors.
Signature Tokens. Prior work [BS17] defines and constructs signature tokens which are signatures which involve a quantum signing token which can only be used once before it becomes inert. The setting they consider is where a client wishes to delegate the signing process to a server, but does not wish the server to be able to sign more than one message. They rely on quantum money [AC13] and the no-cloning principle to ensure the signature can only be computed once. For our unclonable signatures of knowledge result, we focus on the setting where a client wishes to authenticate themselves to a server and wants to prevent an adversary from simultaneously, or later, masquerading as them.
One-shot Signatures. The authors of [AGKZ20] introduce the notion of one-shot signatures which extend the concept of signature tokens to a scenario where the client and server only exchange classical information to create a one-use quantum signature token. They show that these signatures can be plausibly constructed in the CRS model from post-quantum indistinguishability obfuscation. Unless additional measures for security, which we discussed in our applications section, are employed, classical communication can be easily copied and replayed at a later point. In contrast, we prevent an adversary from simultaneously, or later, authenticating with the client’s identity.
Post-quantum Fiat-Shamir. Our QROM results are heavily inspired by the recent post-quantum Fiat-Shamir result [LZ19] which proves the post-quantum security of NIZKs in the compressed quantum(-accessible) random oracle model (compressed QROM). These classical NIZKs are the result of applying Fiat-Shamir to post-quantum sigma protocols which are HVZKPoKs. We further extend, and crucially rely upon, their novel proof techniques to prove extractability (for PoK) and programmability (for ZK) to achieve extractability and programmability for some protocols which output quantum proofs.

