This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Ruta Jawale;
(2) Dakshita Khurana.
Table of Links
Unclonable Non-Interactive Zero-Knowledge in the CRS Model
Unclonable NIZK in the Quantum Ramdon Oracle Model
Unclonable Signatures of Knowledge
5 Unclonable NIZK in the Quantum Random Oracle Model
5.1 A Modified Sigma Protocol
We will begin by introducing a slightly modified sigma protocol. In the coming sections, our construction will involve applying Fiat-Shamir to this modified protocol.

Proof. Perfect completeness This follows directly from the perfect completeness of Π.

and any x with associated λ ∈ N satisfying
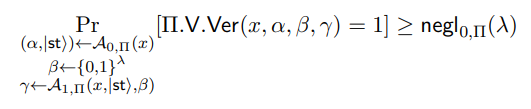
we have
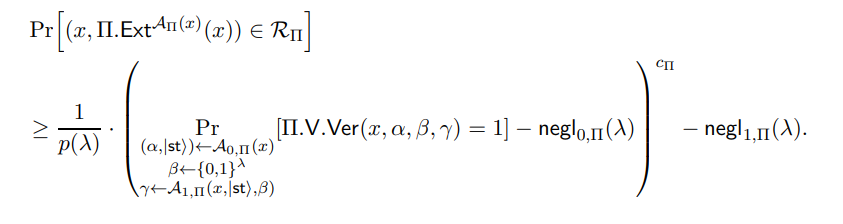
We define Ext 3 with oracle-access to Π.Ext and some A as follows:
Input: x, S.
(1) Given (x, α, s) from AΠ: send α to Π.Ext, receive β from Π.Ext, and send β to AΠ.
(2) Upon receiving γ from AΠ: send γ to Π.Ext.
(3) Output the result of Π.Ext as w.
We define the following set of parameters: c = cΠ, p(·) = pΠ(·), negl0 (·) = negl0,Π(·) and negl1 (·) = negl1,Π(·).
Let polynomial-size quantum circuit A = (A 0, A 1) and (x, S) be given such that
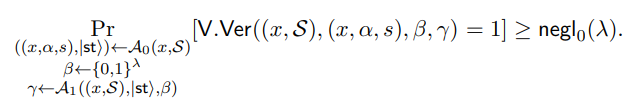
We now define AΠ = (A0,Π, A1,Π) with oracle-access to A. A0,Π is hardwired with S, takes input x, sends (x, S) to A0, receives ((x, α, s), |sti) from A0, and outputs (α, |sti). A1,Π is hardwired with S, takes input (x, |sti, β), sends ((x, S), |sti, β) to A1, receives γ from A1, outputs γ. By the structure of our proof and definition of our verifier, this means that
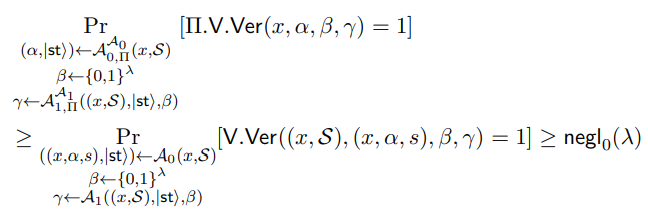
which satisfies the constraint in Equation (15). This means we have, when combined with our definition of Ext, that
Thus showing that our protocol is a proof of knowledge protocol.
Computational Honest-Verifier Zero-Knowledge with Quantum Simulator. Let Π.Sim be the computational honest-verifier zero-knowledge quantum simulator for Π. We define Sim with oracle access to Π.Sim as follows:
Input: x, S.
(1) Compute (α, β, γ) ← Π.Sim(1λ , x)
(2) Sample s from S.
(3) Output ((x, α, s), β, γ).
Let a polynomial p(·), a polynomial-size quantum circuit D, λ ∈ N, and ((x, S), w) ∈ R be given such that
We define a reduction to the zero-knowledge property of Π as follows:
Reduction: to zero-knowledge of Π given oracle access to D.
Hardwired with: x, S.
(1) Receive (real or simulated) (α, β, γ) from the challenger.
(2) Sample s from S.
(3) Send ((x, α, s), β, γ) to D. Receive b from D.
(4) Output b.
When the challenger sends a real (or simulated) proof for Π, the reduction generates a proof that is identical to the real (resp. simulated) proof. As such, this reduction preserves the distinguishing advantage of D. This reaches a contradiction against the zero-knowledge property of Π. Hence, our protocol must be zero-knowledge.
By the definition of the honest prover P.Com,
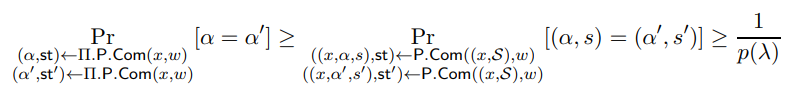
which is a contradiction. Hence our protocol must have unpredictable commitments.
Corollary 5.2. The Fiat-Shamir heuristic applied to the post-quantum sigma protocol defined in Theorem 5.1 yields a classical post-quantum NIZKPoK Π′ in the QROM (Definition 3.11).
Proof. This follows by Theorem 5.1 and Theorem 3.12.
5.2 Unclonability Definitions
Unclonable NIZKs in the quantum random oracle model are defined analogously to the CRS model – we repeat these definitions in the QRO model for completeness below.
Definition 5.3. (Unclonable Security for Hard Instances). A proof (P,V) satisfies unclonable security with respect to a quantum random oracle O if for every language L with corresponding relation RL, for every polynomial-sized quantum circuit family {Cλ}λ∈N, and for every hard distribution {Xλ,Wλ}λ∈N over RL, there exists a negligible function negl1 (·) such that for every λ ∈ N,
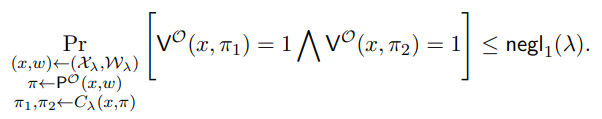
Definition 5.4 ((k−1)-to-k-Unclonable Extractable NIZK in QROM). Let security parameter λ ∈ N and NP relation R with corresponding language L be given. Let Π = (P,V) be given such that P and V are poly(λ)-size quantum algorithms. We have that for any (x, ω) ∈ R, P receives an instance and witness pair (x, ω) as input and outputs π, and V receives an instance x and proof π as input and outputs a value in {0, 1}.
Π is a non-interactive (k − 1)-to-k-unclonable NIZKPoK protocol for language L with respect to a random oracle O if the following holds:
• Π is a NIZKPoK protocol for language L in the quantum random oracle model (Definition 3.11).
• (k−1)-to-k-Unclonable with Extraction: There exists an oracle-aided polynomial-size quantum circuit E such that for every polynomial-size quantum circuit A, for every tuple of k − 1 instance-witness pairs (x1, ω1), . . . ,(xk−1, ωk−1) ∈ R, for every x where we define
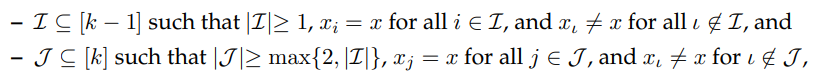
such that there is a polynomial p(·) where
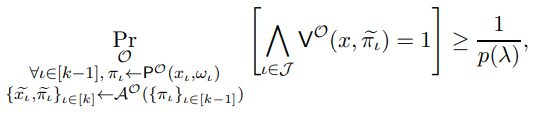
then there is also a polynomial q(·) such that

Similar to the previous section, we have the following lemma.
Lemma 5.5. Let Π = (Setup, P,V) be a a non-interactive 1-to-2-unclonable zero-knowledge quantum protocol (Definition 5.4). Then, Π satisfies Definition 5.3.
For a proof of Lemma 5.5, we refer to Appendix A.
5.3 Unclonable NIZK Implies Public-Key Quantum Money in QROM

Theorem 5.6. Let O be a quantum random oracle. Let (X ,W) be a hard distribution over a language L ∈ NP. Let Π = (P,V) be a 1-to-2 unclonable non-interactive perfectly complete, computationally zero-knowledge protocol for L in the QRO model (Definition 5.4).
Then (P,V) implies a public-key quantum money mini-scheme in the QRO model (Definition 3.15) as described in Figure 4.
Proof. Perfect Correctness. This follows directly from the perfect completeness of Π. Unforgeability. Let p(·) be a polynomial and A be a quantum polynomial-time adversary such that for an infinite number of λ ∈ N +,
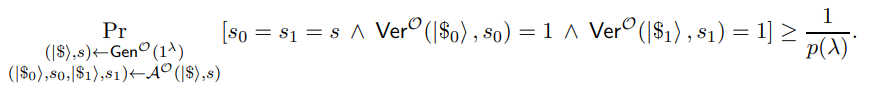
We construct a reduction that breaks the uncloneability definition (Definition 5.3) which we show (in Appendix A) is implied by our definition (Definition 5.4). The challenger, with access to random oracle O, samples a hard instance-witness pair (x, w) ← (X ,Y) and a proof π ← P O(x, w). The challenger then forwards (x, π) to the reduction, which also has oracle access to O. The reduction then sets |$i = π and s = x. The reduction sends (|$i, s) to the adversary A who returns back (|$0, s0, |$1, s1). The reduction then parses and sets πi = |$ii for i ∈ {0, 1}. The reduction then sends π0 and π1 back to the challenger.

5.4 Construction and Analysis
Lemma 5.7. Let λ, k ∈ N and a public-key quantum money mini-scheme (NoteGen,Ver) be given. Let points q1, . . . , qk with the following structure be given: a point q contains a serial number s sampled according to NoteGen(1λ ).
The points q1, . . . , qk must be distinct with overwhelming probability.
Proof. Each point contains a serial number sampled according to the quantum money generation algorithm, NoteGen(1λ ). By the unpredictability of the serial numbers of quantum money (Definition 3.13), all k honestly generated serial numbers must be distinct with overwhelming probability. Hence, these k points will be distinct with overwhelming probability.
We now introduce our construction in Figure 5 and prove the main theorem of this section.
Theorem 5.8. Let k(·) be a polynomial. Let NP relation R with corresponding language L be given.
Let (NoteGen, Ver) be a public-key quantum money mini-scheme (Definition 3.13) and Π = (P,V) be a post-quantum sigma protocol (Definition 3.4).
(P,V) as defined in Figure 5 will be a non-interactive knowledge sound, computationally zero-knowledge, and (k − 1)-to-k-unclonable with extraction protocol for L in the quantum random oracle model (Definition 3.11).
Proof. Let the parameters and primitives be as given in the theorem statement. We argue that completeness follows from the protocol construction in Figure 5, and we prove the remaining properties below.
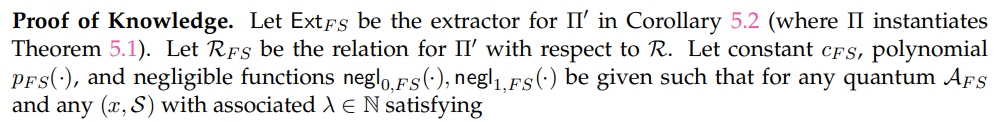
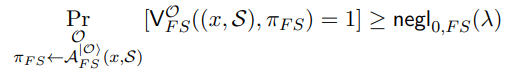

we have
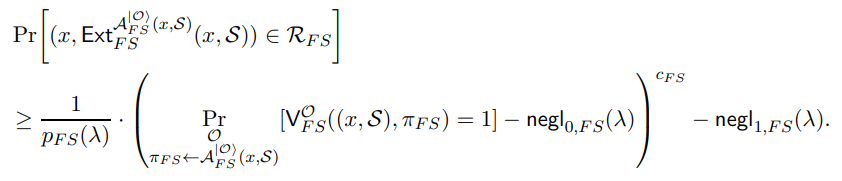

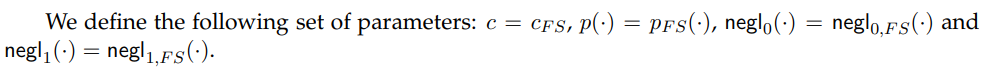
Let polynomial-size quantum circuit A and x be given such that
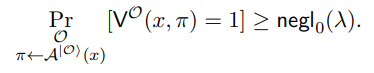
Let AF S be defined with oracle-access to some A and O as follows:
Input: x, S.
(1) Given a query (x, α, s) from A: send (x, α, s) to O, receive β from O, and send β to A.
(2) Upon receiving π = (|$i, s, α, β, γ) from A: output πF S = ((x, α, s), β, γ).
By the structure of our proof and definition of our verifier, this means that
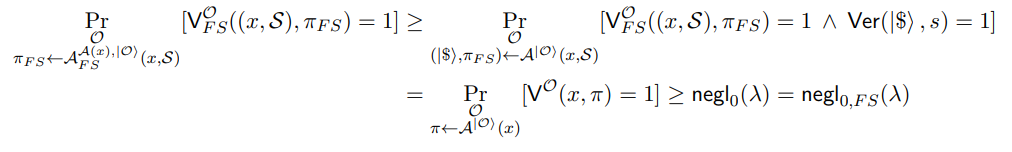
which satisfies the constraint in Equation (16). This means we have, when combined with our definition of Ext and S, that
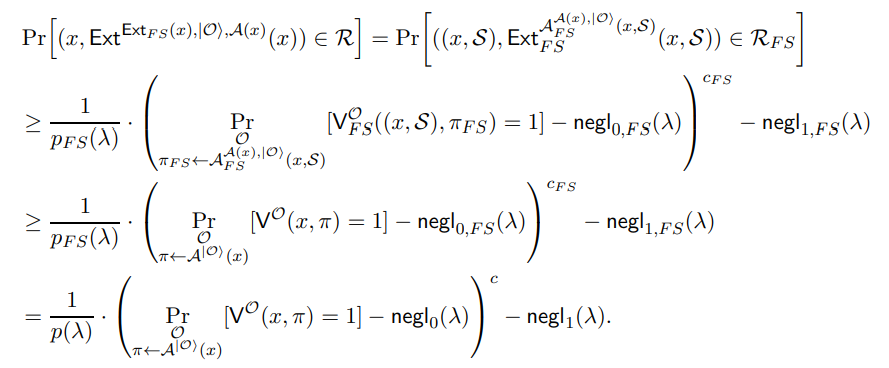
Thus showing that our protocol is a proof of knowledge protocol.
Zero-Knowledge. Let SimF S be the simulator for Π′ in Corollary 5.2 (where Π instantiates Theorem 5.1). Let RF S be the relation for Π′ with respect to R. We define Sim with oracle-access to SimF S and program access to some random oracle O as follows:
Input: x (ignores any witnesses it may receive).

Let an oracle-aided distinguisher D which can only make queries (x, w) ∈ R, and a polynomial p(·) be given such that
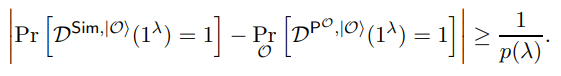
We define a reduction to the zero-knowledge property of Π′ as follows:
Reduction: to zero-knowledge of Π′ given oracle access to D and program access to O.
For every (x, w) from D:

The view of D matches that of our protocol in Figure 5 or Sim. As such, our reduction should have the same advantage at breaking the zero-knowledge property of Π′ . We reach a contradiction, hence our protocol must be zero-knowledge.
Unclonable Extractability. Let Ext be the quantum circuit of the extractor we defined earlier (in our proof that Figure 5 is a proof of knowledge). Let Sim be the quantum circuit of the simulator that we defined earlier (in our proof that Figure 5 is a zero-knowledge protocol). We define an extractor E with oracle-access to some A as follows:
Hardwired with: some choice of I ⊆ [k − 1], J ⊆ [k], x1, . . . , xk−1 ∈ R, x.
(1) Samples ℓ ∈ J uniformly at random.
(2) Instantiates a simulatable and extractable random oracle O. Runs Ext on O throughout the interaction with A (which may involve rewinding, in which case we would rewind A and repeat the following steps). Require that Ext extracts with respect to the ℓth proof output by A.
(3) Compute πι ← Sim(xι) for ι ∈ [k − 1] where we store all points Sim would program into a list P.
(4) Send {πι}ι∈[k−1] to A.
(5) For every query from A, if the query is in P, then reply with the answer from P. Else, forward the query to O and send the answer back to A. Let Ob denote this modified random oracle.
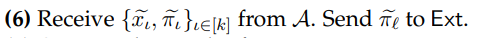
(7) Outputs the result of Ext as w.
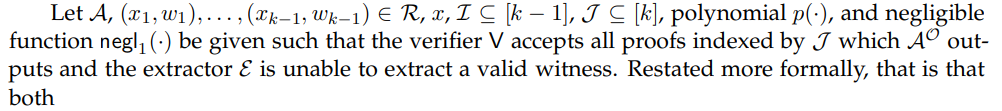
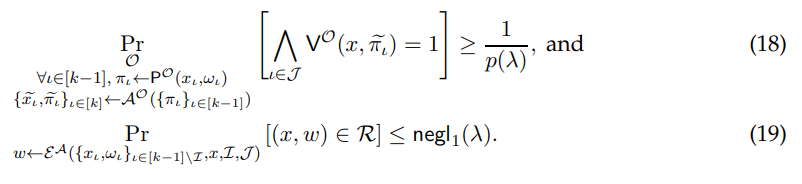
Given Equation (24), we may be in one of the two following cases: either A generates two accepting proofs which have the same serial number as a honestly generated proof, or A does not. We consider these two scenarios separately and show that each reaches a contradiction.
Scenario One
Say that A generates two accepting proofs which have the same serial number as an honestly generated proof. By applying a union bound to Equation (24), we have that this event could happen with at least 1/2p(λ) probability. Symbolically,
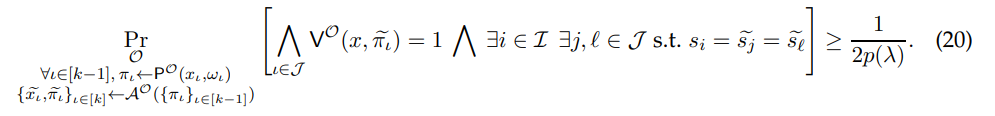

Scenario Two
Alternatively, say that A does not generate two accepting proofs which have the same serial number as an honestly generated proof. By the pigeon-hole principle, this means that A generates an accepting proof with a serial number which is not amongst the ones it received. By applying a union bound to Equation (24), we have that this event could happen with at least 1/2p(λ) probability. In summary, we have that
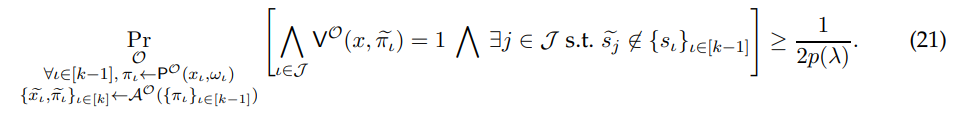
Through an averaging argument, we can fix index j ∈ J which gives us the same event with an advantage of 1/(2kp(λ)). We will now switch to a hybrid where we provide A with simulated proofs at indices I.
Claim 5.9. There exists a polynomial q(·) such that
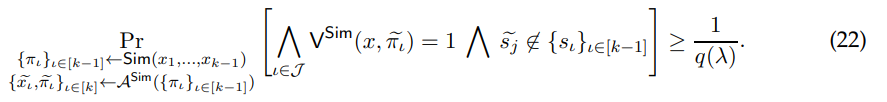
We will later see a proof of Claim 5.9. For now, assuming that this claim holds, we can define an adversary from which Ext can extract a valid witness for x.
Claim 5.10. There exists a polynomial q ′ (·) such that
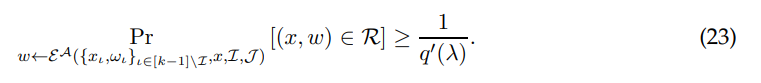
We will soon see a proof for Claim 5.10. Meanwhile, if this claim is true, then we will have a direct contradiction with Equation (19). Thus, all that remains to be proven are the two claims: Claim 5.9 and Claim 5.10. We start by proving the former claim.
Proof of Claim 5.9. We first need to argue that our strategy is well-defined, that we will be able to independently program these k points. Then we can argue the indistinguishability of switching one-by-one to simulated proofs. We will argue that our simulator will run in expected polynomial time. By Lemma 5.7, the k points which our simulator will program will be distinct with overwhelming probability. Furthermore, since we assumed that our quantum random oracle can be programmed at multiple distinct points Definition 3.10, our simulator is well-defined.
We now argue indistinguishability of the simulated proofs from the honestly generated proofs via a hybrid argument. Suppose for sake of contradiction that the probability difference between Equation (21) and Equation (22) was 1/p′ (λ) for some polynomial p ′ (·). We construct a series of consecutive hybrids for each i ∈ [k − 1] where we switch the i th proof from prover generated to simulated. By this hybrid argument, there must be some position ℓ ∈ [k − 1] where switching the ℓ th proof has a probability difference of at least 1/(kp′ (λ)). We now formalize a reduction which can distinguish between these two settings:

We first argue that the view that the reduction provides to A matches one of the games: where all proofs up to the ℓ th are simulated or where all proofs up to and including the ℓ th are simulated. By Lemma 5.7, the point computed or programmed by the challenger will be distinct from the points which the reduction programs. As such, the reduction is allowed to modify 5 the oracle which A interfaces with (see step (4)). In summary, A will be provided access to an oracle that is consistent with all of the proofs it receives.
Given that A has a view which directly matches its expected view in either game, then the reduction’s advantage is the same as A’s advantage which is at least 1/(kp′ (λ)). This is a contradiction with the zero-knowledge property of our protocol. Thus, our original claim must be true.
Now, we continue on to proving the latter claim.
Proof of Claim 5.10. Given that Claim 5.9 holds, this implies that
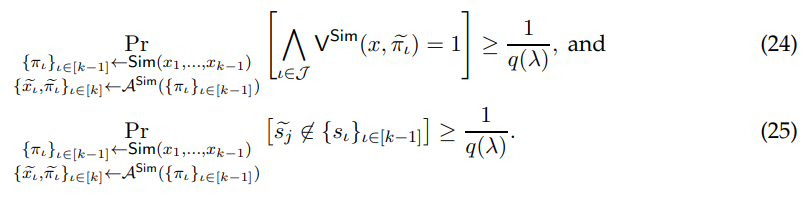

First we must argue that A’s view remains identical to the game which appears in both Equation (24) and Equation (25). The oracle which A interfaces with (see step (4)) will be consistent with all of the proofs it receives.
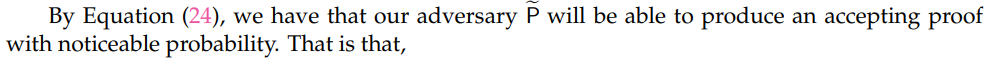
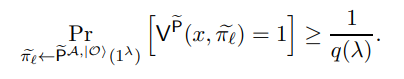

Through Equation (25), we reach the conclusion that
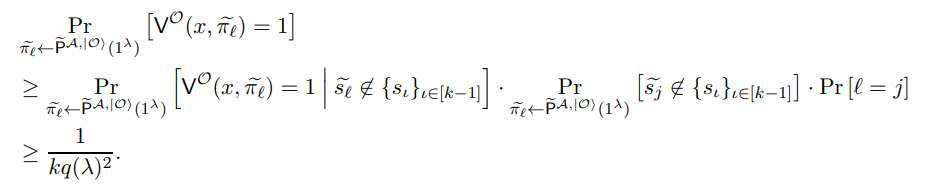
By the definition of a proof of knowledge (Definition 3.11) which have some parameters polynomial p ∗ (·) and negligible functions negl0 (·) and negl1 (·), we have that there exists some polynomial q ′ (·) such that
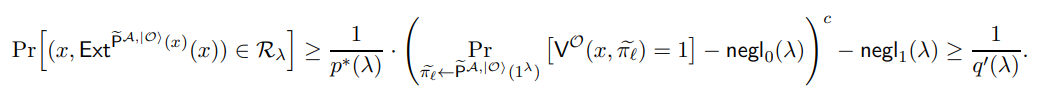
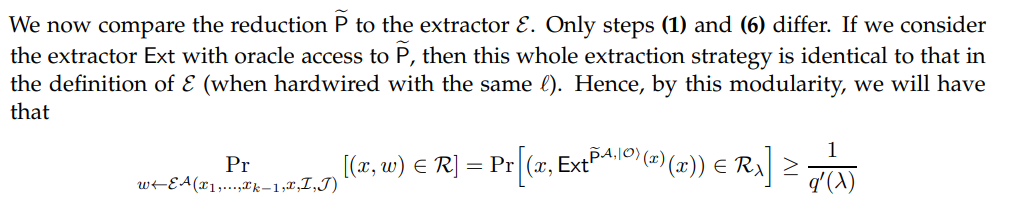
which completes the proof of our claim.
By completing the proofs of our claims, we have concluding the proof of our theorem statement.
Corollary 5.11. Assuming the injective one-way functions exist, and post-quantum iO exists, there exists a non-interactive knowledge sound, computationally zero-knowledge, and (k − 1)-to-kunclonable with extraction protocol for NP in the quantum random oracle model (Definition 5.4).
Proof. This follows from Theorem 3.14 and Theorem 5.8.
We have thus shown that Figure 5 is an unclonable NIZK PoK in the ROM model as defined according to our unclonability definition, Definition 5.4.

