This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Ruta Jawale;
(2) Dakshita Khurana.
Table of Links
Unclonable Non-Interactive Zero-Knowledge in the CRS Model
Unclonable NIZK in the Quantum Ramdon Oracle Model
Unclonable Signatures of Knowledge
3 Preliminaries
3.1 Post-Quantum Commitments and Encryption
Definition 3.1 (Post-Quantum Commitments). Com is a post-quantum commitment scheme if it has the following syntax and properties.
Syntax.
• c ← Com(m; r): The polynomial-time algorithm Com on input a message m and randomness r ∈ {0, 1} r(λ) outputs commitment a c.
Properties.
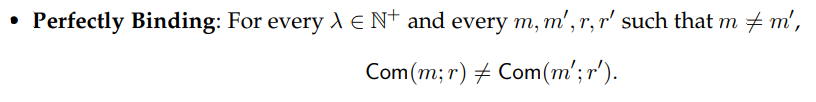

Theorem 3.2 (Post-Quantum Commitment). [LS19] Assuming the polynomial quantum hardness of LWE, there exists a non-interactive commitment with perfect binding and computational hiding (Definition 3.1).
Definition 3.3 (Post-Quantum Public-Key Encryption). (Gen, Enc, Dec) is a post-quantum publickey encryption scheme if it has the following syntax and properties.
Syntax.
• (pk,sk) ← Gen(1λ ): The polynomial-time algorithm Gen on input security parameter 1 λ outputs a public key pk and a secret key sk.
• c ← Enc(pk, m; r): The polynomial-time algorithm Enc on input a public key pk, message m and randomness r ∈ {0, 1} r(λ) outputs a ciphertext c.
• m ← Dec(sk, c): The polynomial-time algorithm Dec on input a secret key sk and a ciphertext c outputs a message m.
Properties.
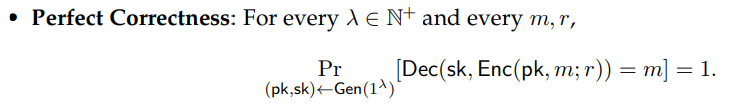

3.2 Sigma protocols
Definition 3.4 (Post-Quantum Sigma Protocol for NP). [LZ19] Let NP relation R with corresponding language L be given such that they can be indexed by a security parameter λ ∈ N.
Π = (P = (P.Com, P.Prove),V = (V.Ch,V.Ver)) is a post-quantum sigma protocol if it has the following syntax and properties.
Syntax. The input 1 λ is left out when it is clear from context.
• (α,st) ← P.Com(1λ , x, w): The probabilistic polynomial-size circuit P.Com on input an instance and witness pair (x, w) ∈ Lλ outputs a commitment α and an internal prover state st.
• β ← V.Ch(1λ , x, α): The probabilistic polynomial-size circuit V.Ch on input an instance x outputs a uniformly random challenge β.
• γ ← P.Prove(1λ , x, w,st, β): The probabilistic polynomial-size circuit P. Prove on input an instance and witness pair (x, w) ∈ Lλ, an internal prover state st, and a challenge β outputs the partial opening (to α as indicated by β) γ.
• V. Ver(1λ , x, α, β, γ) ∈ {0, 1}: The probabilistic polynomial-size circuit V.Ver on input an instance x, a commitment α, a challenge β, and a partial opening γ outputs 1 iff γ is a valid opening to α at locations indicated by β.
Properties.
• Perfect Completeness. For every λ ∈ N and every (x, w) ∈ Rλ,

• Computational Honest-Verifier Zero-Knowledge with Quantum Simulator. There exists a quantum polynomial-size circuit Sim and a negligible function negl(·) such that for every polynomial-size quantum circuit D, every sufficiently large λ ∈ N, and every (x, w) ∈ Rλ,
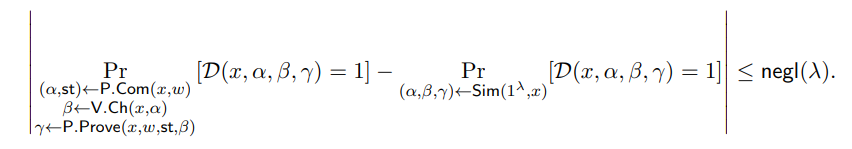

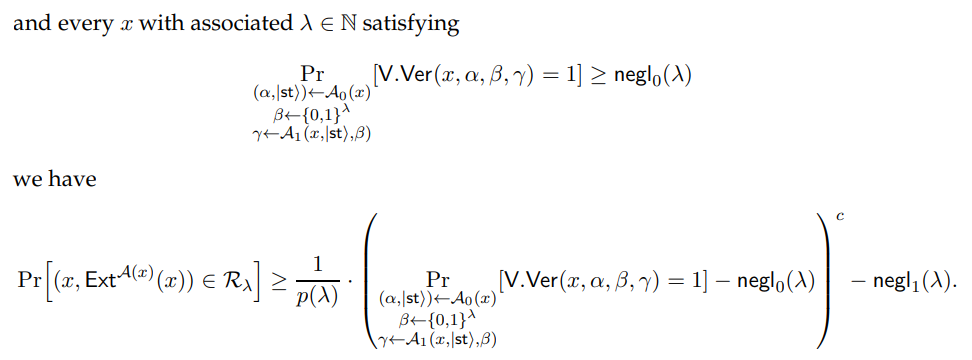
• Unpredictable Commitment. There exists a negligible function negl(·) such that for every sufficiently large λ ∈ N and every (x, w) ∈ Rλ,
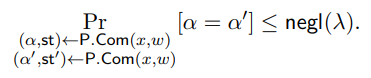
We note that the unpredictable commitment property in the definition above may appear to be an unusual requirement, but this property is w.l.o.g. for post quantum sigma protocols as shown in [LZ19]. In particular, any sigma protocol which does not have unpredictable commitments, can be modified into one that does: the prover can append a random string r to the end of their commitment message α, and the verifier can ignore this appended string r when they perform their checks.
3.3 NIZKs in the CRS model
We consider the common reference string model.
Definition 3.5 (Post-Quantum (Quantum) NIZK for NP in the CRS Model). Let NP relation R with corresponding language L be given such that they can be indexed by a security parameter λ ∈ N
Π = (Setup, P,V) is a non-interactive post-quantum (quantum) zero-knowledge argument for NP in the CRS model if it has the following syntax and properties.
Syntax. The input 1 λ is left out when it is clear from context.
• crs ← Setup(1λ ): The probabilistic polynomial-size circuit Setup on input 1 λ outputs a common reference string crs.
• π ← P(1λ , crs, x, w): The probabilistic (quantum) polynomial-size circuit P on input a common reference string crs and instance and witness pair (x, w) ∈ Rλ, outputs a proof π.
• V(1λ , crs, x, π) ∈ {0, 1}: The probabilistic (quantum) polynomial-size circuit V on input a common reference string crs, an instance x, and a proof π outputs 1 iff π is a valid proof for x.
Properties.
• Perfect Completeness. For every λ ∈ N and every (x, w) ∈ Rλ,
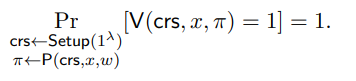
• Adaptive Computational Soundness. There exists a negligible function negl(·) such that for every polynomial-size quantum circuit A and every sufficiently large λ ∈ N,
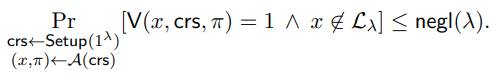
• Adaptive Computational Zero-Knowledge. There exists a probabilistic (quantum) polynomial-size circuit Sim = (Sim0, Sim1) and a negligible function negl(·) such that for every polynomial-size quantum circuit A, every polynomial-size quantum circuit D, and every sufficiently large λ ∈ N,
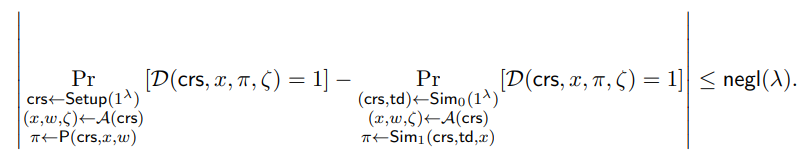
Theorem 3.6 (Post-Quantum NIZK argument for NP in the CRS Model). [PS19] Assuming the polynomial quantum hardness of LWE, there exists a non-interactive adaptively computationally sound, adaptively computationally zero-knowledge argument for NP in the common reference string model (Definition 3.5).
Definition 3.7 (Post-Quantum (Quantum) Simulation-Sound NIZK for NP in CRS Model). Let NP relation R with corresponding language L be given such that they can be indexed by a security parameter λ ∈ N
Π = (Setup, P,V) is a post-quantum (quantum) non-interactive simulation-sound, adaptive multi-theorem computational zero-knowledge protocol for NP in the CRS model if it has the following syntax and properties.
• Π is a post-quantum (quantum) non-interactive zero-knowledge argument for NP in the CRS model (Definition 3.5).
• Adaptive Multi-Theorem Computational Zero-Knowledge. [FLS90] There exists a probabilistic (quantum) polynomial-size circuit Sim = (Sim0, Sim1) 1 and a negligible function negl(·) such that for every polynomial-size quantum circuit A, every polynomial-size quantum circuit D, and every sufficiently large λ ∈ N,
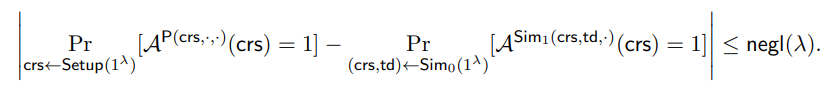
• Simulation Soundness. [Sah99, SCO+01] Let Sim = (Sim0, Sim1) be the simulator given by the adaptive multi-theorem computational zero-knowledge property. There exists a negligible function negl(·) such that for every oracle-aided polynomial-size quantum circuit A and every sufficiently large λ ∈ N,
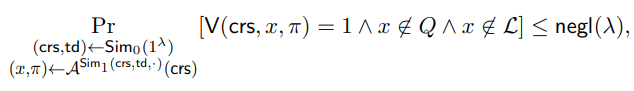
where Q is the list of queries from A to Sim1.
REMARK 3.1. In Definition 3.7, adaptive multi-theorem computational zero-knowledge implies adaptive computational zero-knowledge.
REMARK 3.2. As defined in Definition 3.7, a simulation-sound zero-knowledge protocol has adaptive computational soundness (Definition 3.5).
Theorem 3.8 (Simulation Sound Compiler). [SCO+01] Given one-way functions and a single-theorem NIZK proof system for NP, then there exists a non-interactive simulation sound, adaptively multi-theorem computationally zero-knowledge proof for NP in the common reference string model (Definition 3.7).
Corollary 3.9 (Post-Quantum Simulation Sound NIZK for NP). Assuming the polynomial quantum hardness of LWE, there exists a post-quantum non-interactive simulation sound, adaptively multi-theorem computationally zero-knowledge proof for NP in the common reference string model (Definition 3.7).
Proof. This follows from Theorem 3.6 and Theorem 3.8.
3.4 NIZKs in the QRO model
We now consider the quantum random oracle model. For sake of completeness, we briefly outline a definition for a quantum random oracle.
Definition 3.10. A quantum random oracle O is a random function which support quantum queries and allows for the following accesses:
• Query Access. On input a message, O outputs a uniformly random value. This is the usual access provided. When quantum access may be invoked, we denote the oracle as |O.
• Programmability Access. Given programmability access, O can be set to output a specified value on a specified input. An arbitrary number of distinct points can be programmed.
• Extractability Access. Given extractability access, specific queries to |O can be read.
Definition 3.11 ((Quantum) Post-Quantum NIZKPoK for NP in QROM). [LZ19] Let O be a random oracle. Let NP relation R with corresponding language L be given such that they can be indexed by a security parameter λ ∈ N.
Π = (P,V) is a (quantum) non-interactive zero-knowledge proof of knowledge protocol with respect to a random oracle if it has the following syntax and properties.
Syntax. The input 1 λ is left out when it is clear from context.

Properties.
• Perfect Completeness. For every λ ∈ N and every (x, w) ∈ Rλ,
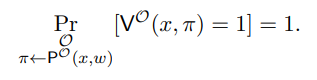
• Zero-Knowledge with Quantum Simulator. There exists a quantum polynomial-size circuit Sim which ignores its second input and a negligible function negl(·) such that for every oracle-aided polynomial-size quantum circuit D which is limited to making queries (x, ω) ∈ Rλ on input 1 λ , and every sufficiently large λ ∈ N,
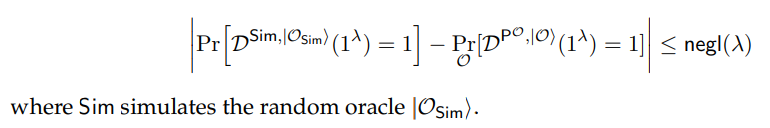
• Proof of Knowledge with Quantum Extractor. There exists an oracle-aided quantum polynomial-size circuit extractor Ext that simulates a random oracle |OExti, a constant c, a polynomial p(·), and negligible functions negl0 (·), negl1 (·) such that for every polynomial-size quantum circuit A and every x with associated λ ∈ N satisfying
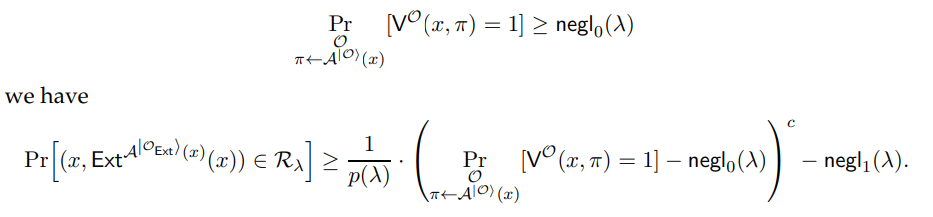
Theorem 3.12 (NIZKPoK in QROM [Unr17, LZ19]). Let Π be a post-quantum sigma protocol (Definition 3.4). The Fiat-Shamir heuristic applied to Π yields a classical post-quantum NIZKPoK in the QROM (Definition 3.11).
3.5 Quantum Money
Definition 3.13 (Public Key Quantum Money Mini-Scheme). [AC13, Zha19b] (Gen,Ver) is a public key quantum money scheme if it has the following syntax and properties.
Syntax.
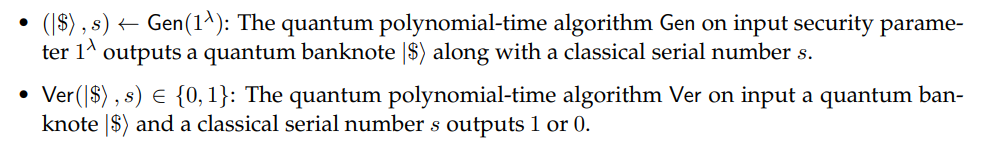
Properties.
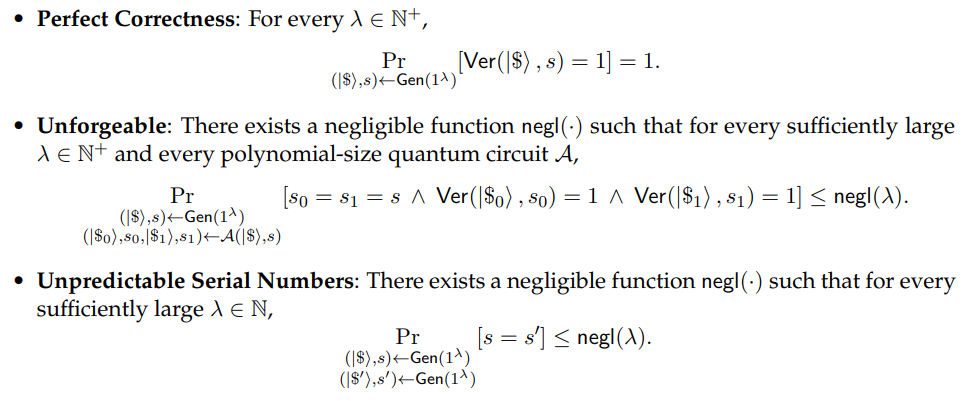

Theorem 3.14 (Quantum Money from Subspace Hiding Obfuscation [AC13, Zha19b]). If injective one-way functions and post-quantum iO exist, then public-key quantum money exists (Definition 3.13).
Definition 3.15 (Public Key Quantum Money Mini-Scheme in QROM). (Gen, Ver) is a public key quantum money scheme with respect to a quantum random oracle O if it has the following syntax and properties.
Syntax.

Properties
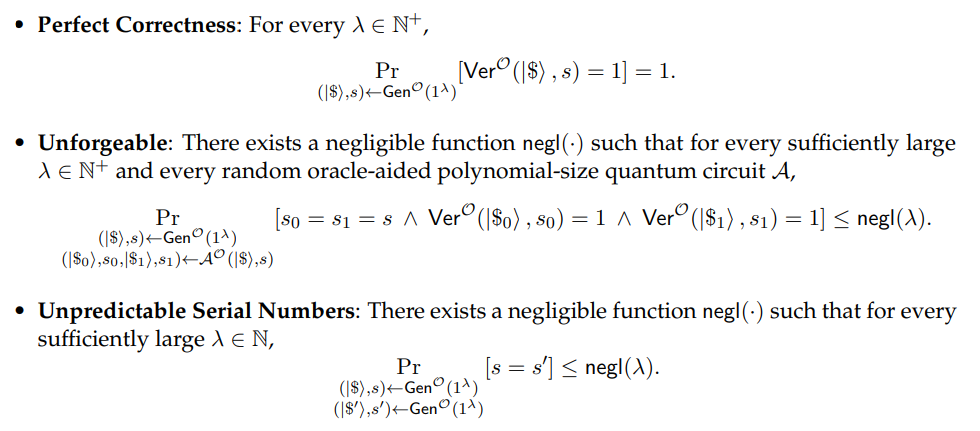
The unpredicable serial number property is w.l.o.g., just as above.
3.6 Quantum Signature of Knowledge
Definition 3.16 (Quantum SimExt-secure Signature [CL06]). Let NP relation R with corresponding language L be given such that they can be indexed by a security parameter λ ∈ N. Let a message space M be given such that it can be indexed by a security parameter λ ∈ N.
(Setup, Sign, Verify) is a SimExt-secure quantum signature of knowledge of a witness with respect to L and M if it has the following syntax and properties. Syntax. The input 1 λ is left out when it is clear from context.
• (crs, td) ← Setup(1λ ): The probabilistic polynomial-time algorithm Setup on input 1 λ outputs a common reference string crs and a trapdoor td.
• σ ← Sign(1λ , crs, x, w, m): The polynomial-time quantum algorithm Sign on input a common reference string crs, an instance and witness pair (x, w) ∈ Rλ, and a message m ∈ Mλ, outputs a signature σ.
• Verify(1λ , crs, x, m, σ) ∈ {0, 1}: The polynomial-time quantum algorithm Verify on input a common reference string crs, an instance x, a message m ∈ Mλ, and a signature σ, outputs 1 iff σ is a valid signature of m with respect to crs, Rλ, and x.
Properties.


