This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Ruta Jawale;
(2) Dakshita Khurana.
Table of Links
Unclonable Non-Interactive Zero-Knowledge in the CRS Model
Unclonable NIZK in the Quantum Ramdon Oracle Model
Unclonable Signatures of Knowledge
References
[Aar09] Scott Aaronson. Quantum copy-protection and quantum money. In Proceedings of the 24th Annual IEEE Conference on Computational Complexity, CCC 2009, Paris, France, 15-18 July 2009, pages 229–242. IEEE Computer Society, 2009.
[AC13] Scott Aaronson and Paul F. Christiano. Quantum money from hidden subspaces. Theory Comput., 9:349–401, 2013. [AGKZ20] Ryan Amos, Marios Georgiou, Aggelos Kiayias, and Mark Zhandry. One-shot signatures and applications to hybrid quantum/classical authentication. In Konstantin Makarychev, Yury Makarychev, Madhur Tulsiani, Gautam Kamath, and Julia Chuzhoy, editors, Proccedings of the 52nd Annual ACM SIGACT Symposium on Theory of Computing, STOC 2020, Chicago, IL, USA, June 22-26, 2020, pages 255–268. ACM, 2020.
[AK21] Prabhanjan Ananth and Fatih Kaleoglu. Unclonable encryption, revisited. In Kobbi Nissim and Brent Waters, editors, Theory of Cryptography - 19th International Conference, TCC 2021, Raleigh, NC, USA, November 8-11, 2021, Proceedings, Part I, volume 13042 of Lecture Notes in Computer Science, pages 299–329. Springer, 2021.
[AKL+22] Prabhanjan Ananth, Fatih Kaleoglu, Xingjian Li, Qipeng Liu, and Mark Zhandry. On the feasibility of unclonable encryption, and more. In Yevgeniy Dodis and Thomas Shrimpton, editors, Advances in Cryptology - CRYPTO 2022 - 42nd Annual International Cryptology Conference, CRYPTO 2022, Santa Barbara, CA, USA, August 15-18, 2022, Proceedings, Part II, volume 13508 of Lecture Notes in Computer Science, pages 212–241. Springer, 2022.
[ALL+21] Scott Aaronson, Jiahui Liu, Qipeng Liu, Mark Zhandry, and Ruizhe Zhang. New approaches for quantum copy-protection. In Tal Malkin and Chris Peikert, editors, Advances in Cryptology - CRYPTO 2021 - 41st Annual International Cryptology Conference, CRYPTO 2021, Virtual Event, August 16-20, 2021, Proceedings, Part I, volume 12825 of Lecture Notes in Computer Science, pages 526–555. Springer, 2021.
[AN11] Tolga Acar and Lan Nguyen. Revocation for delegatable anonymous credentials. In Dario Catalano, Nelly Fazio, Rosario Gennaro, and Antonio Nicolosi, editors, Public Key Cryptography - PKC 2011 - 14th International Conference on Practice and Theory in Public Key Cryptography, Taormina, Italy, March 6-9, 2011. Proceedings, volume 6571 of Lecture Notes in Computer Science, pages 423–440. Springer, 2011.
[AP21] Prabhanjan Ananth and Rolando L. La Placa. Secure software leasing. In Anne Canteaut and Franc¸ois-Xavier Standaert, editors, Advances in Cryptology - EUROCRYPT 2021 - 40th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zagreb, Croatia, October 17-21, 2021, Proceedings, Part II, volume 12697 of Lecture Notes in Computer Science, pages 501–530. Springer, 2021.
[BCC+09] Mira Belenkiy, Jan Camenisch, Melissa Chase, Markulf Kohlweiss, Anna Lysyanskaya, and Hovav Shacham. Randomizable proofs and delegatable anonymous credentials. In Shai Halevi, editor, Advances in Cryptology - CRYPTO 2009, 29th Annual International Cryptology Conference, Santa Barbara, CA, USA, August 16-20, 2009. Proceedings, volume 5677 of Lecture Notes in Computer Science, pages 108–125. Springer, 2009.
[BGG+23] James Bartusek, Sanjam Garg, Vipul Goyal, Dakshita Khurana, Giulio Malavolta, Justin Raizes, and Bhaskar Roberts. Obfuscation and outsourced computation with certified deletion. Cryptology ePrint Archive, Paper 2023/265, 2023. [BI20] Anne Broadbent and Rabib Islam. Quantum encryption with certified deletion. In Rafael Pass and Krzysztof Pietrzak, editors, Theory of Cryptography, pages 92–122, Cham, 2020. Springer International Publishing.
[BK23] James Bartusek and Dakshita Khurana. Cryptography with certified deletion. In Crypto 2023 (to appear), 2023.
[BKP23] James Bartusek, Dakshita Khurana, and Alexander Poremba. Publicly-verifiable deletion via target-collapsing functions. In Crypto 2023 (to appear), 2023.
[BL20] Anne Broadbent and S´ebastien Lord. Uncloneable quantum encryption via oracles. In Steven T. Flammia, editor, 15th Conference on the Theory of Quantum Computation, Communication and Cryptography, TQC 2020, June 9-12, 2020, Riga, Latvia, volume 158 of LIPIcs, pages 4:1–4:22. Schloss Dagstuhl - Leibniz-Zentrum f ¨ur Informatik, 2020.
[BS16] Shalev Ben-David and Or Sattath. Quantum tokens for digital signatures. CoRR, abs/1609.09047, 2016.
[BS17] Shalev Ben-David and Or Sattath. Quantum tokens for digital signatures. IACR Cryptol. ePrint Arch., page 94, 2017.
[BS23a] Mohammed Barhoush and Louis Salvail. How to sign quantum messages, 2023.
[BS23b] Mohammed Barhoush and Louis Salvail. Powerful primitives in the bounded quantum storage model, 2023.
[CKS10] Jan Camenisch, Markulf Kohlweiss, and Claudio Soriente. Solving revocation with efficient update of anonymous credentials. In Juan A. Garay and Roberto De Prisco, editors, Security and Cryptography for Networks, 7th International Conference, SCN 2010, Amalfi, Italy, September 13-15, 2010. Proceedings, volume 6280 of Lecture Notes in Computer Science, pages 454–471. Springer, 2010.
[CL06] Melissa Chase and Anna Lysyanskaya. On signatures of knowledge. In Cynthia Dwork, editor, Advances in Cryptology - CRYPTO 2006, 26th Annual International Cryptology Conference, Santa Barbara, California, USA, August 20-24, 2006, Proceedings, volume 4117 of Lecture Notes in Computer Science, pages 78–96. Springer, 2006.
[CLLZ21] Andrea Coladangelo, Jiahui Liu, Qipeng Liu, and Mark Zhandry. Hidden cosets and applications to unclonable cryptography. In Tal Malkin and Chris Peikert, editors, Advances in Cryptology - CRYPTO 2021 - 41st Annual International Cryptology Conference, CRYPTO 2021, Virtual Event, August 16-20, 2021, Proceedings, Part I, volume 12825 of Lecture Notes in Computer Science, pages 556–584. Springer, 2021.
[CW19] Xavier Coiteux-Roy and Stefan Wolf. Proving erasure. In IEEE International Symposium on Information Theory, ISIT 2019, Paris, France, July 7-12, 2019, pages 832–836, 2019.
[FGH+12] Edward Farhi, David Gosset, Avinatan Hassidim, Andrew Lutomirski, and Peter W. Shor. Quantum money from knots. In Shafi Goldwasser, editor, Innovations in Theoretical Computer Science 2012, Cambridge, MA, USA, January 8-10, 2012, pages 276–289. ACM, 2012.
[FLS90] Uriel Feige, Dror Lapidot, and Adi Shamir. Multiple non-interactive zero knowledge proofs based on a single random string (extended abstract). In 31st Annual Symposium on Foundations of Computer Science, St. Louis, Missouri, USA, October 22-24, 1990, Volume I, pages 308–317. IEEE Computer Society, 1990.
[FM18] Honghao Fu and Carl A. Miller. Local randomness: Examples and application. Phys. Rev. A, 97:032324, Mar 2018.
[GMR89] Shafi Goldwasser, Silvio Micali, and Charles Rackoff. The knowledge complexity of interactive proof systems. SIAM J. Comput., 18(1):186–208, 1989.
[Got03] Daniel Gottesman. Uncloneable encryption. Quantum Inf. Comput., 3(6):581–602, 2003.
[GZ20] Marios Georgiou and Mark Zhandry. Unclonable decryption keys. IACR Cryptol. ePrint Arch., page 877, 2020.
[HMNY21] Taiga Hiroka, Tomoyuki Morimae, Ryo Nishimaki, and Takashi Yamakawa. Quantum encryption with certified deletion, revisited: Public key, attribute-based, and classical communication. In Mehdi Tibouchi and Huaxiong Wang, editors, Advances in Cryptology – ASIACRYPT 2021, pages 606–636, Cham, 2021. Springer International Publishing.
[HMNY22] Taiga Hiroka, Tomoyuki Morimae, Ryo Nishimaki, and Takashi Yamakawa. Certified everlasting zero-knowledge proof for QMA. CRYPTO, 2022. https://ia.cr/2021/1315.
[IBM23] IBM. Cost of a data breach report 2023. Technical report, IBM, 2023. [Kan18] Daniel M. Kane. Quantum money from modular forms. CoRR, abs/1809.05925, 2018.
[KN23] Fuyuki Kitagawa and Ryo Nishimaki. One-out-of-many unclonable cryptography: Definitions, constructions, and more. IACR Cryptol. ePrint Arch., page 229, 2023.
[KT20] Srijita Kundu and Ernest Y. Z. Tan. Composably secure device-independent encryption with certified deletion, 2020.
[LS19] Alex Lombardi and Luke Schaeffer. A note on key agreement and noninteractive commitments. Cryptology ePrint Archive, Paper 2019/279, 2019. https://eprint.iacr.org/2019/279.
[LZ19] Qipeng Liu and Mark Zhandry. Revisiting post-quantum fiat-shamir. In Alexandra Boldyreva and Daniele Micciancio, editors, Advances in Cryptology - CRYPTO 2019 - 39th Annual International Cryptology Conference, Santa Barbara, CA, USA, August 18-22, 2019, Proceedings, Part II, volume 11693 of Lecture Notes in Computer Science, pages 326–355. Springer, 2019.
[MST21] Christian Majenz, Christian Schaffner, and Mehrdad Tahmasbi. Limitations on uncloneable encryption and simultaneous one-way-to-hiding. IACR Cryptol. ePrint Arch., page 408, 2021.
[Por22] Alexander Poremba. Quantum proofs of deletion for learning with errors. Cryptology ePrint Archive, Report 2022/295, 2022. https://ia.cr/2022/295. [PS19] Chris Peikert and Sina Shiehian. Noninteractive zero knowledge for NP from (plain) learning with errors. In Alexandra Boldyreva and Daniele Micciancio, editors, Advances in Cryptology - CRYPTO 2019 - 39th Annual International Cryptology Conference, Santa Barbara, CA, USA, August 18-22, 2019, Proceedings, Part I, volume 11692 of Lecture Notes in Computer Science, pages 89–114. Springer, 2019.
[Sah99] Amit Sahai. Non-malleable non-interactive zero knowledge and adaptive chosenciphertext security. In 40th Annual Symposium on Foundations of Computer Science, FOCS ’99, 17-18 October, 1999, New York, NY, USA, pages 543–553. IEEE Computer Society, 1999.
[SCO+01] Alfredo De Santis, Giovanni Di Crescenzo, Rafail Ostrovsky, Giuseppe Persiano, and Amit Sahai. Robust non-interactive zero knowledge. In Joe Kilian, editor, Advances in Cryptology - CRYPTO 2001, 21st Annual International Cryptology Conference, Santa Barbara, California, USA, August 19-23, 2001, Proceedings, volume 2139 of Lecture Notes in Computer Science, pages 566–598. Springer, 2001.
[SCP00] Alfredo De Santis, Giovanni Di Crescenzo, and Giuseppe Persiano. Necessary and sufficient assumptions for non-iterative zero-knowledge proofs of knowledge for all NP relations. In Ugo Montanari, Jos´e D. P. Rolim, and Emo Welzl, editors, Automata, Languages and Programming, 27th International Colloquium, ICALP 2000, Geneva, Switzerland, July 9-15, 2000, Proceedings, volume 1853 of Lecture Notes in Computer Science, pages 451–462. Springer, 2000.
[SP92] Alfredo De Santis and Giuseppe Persiano. Zero-knowledge proofs of knowledge without interaction (extended abstract). In 33rd Annual Symposium on Foundations of Computer Science, Pittsburgh, Pennsylvania, USA, 24-27 October 1992, pages 427–436. IEEE Computer Society, 1992.
[Unr14] Dominique Unruh. Revocable quantum timed-release encryption. In Phong Q. Nguyen and Elisabeth Oswald, editors, Advances in Cryptology - EUROCRYPT 2014 - 33rd Annual International Conference on the Theory and Applications of Cryptographic Techniques, Copenhagen, Denmark, May 11-15, 2014. Proceedings, volume 8441 of Lecture Notes in Computer Science, pages 129–146. Springer, 2014.
[Unr17] Dominique Unruh. Post-quantum security of fiat-shamir. In Tsuyoshi Takagi and Thomas Peyrin, editors, Advances in Cryptology - ASIACRYPT 2017 - 23rd International Conference on the Theory and Applications of Cryptology and Information Security, Hong Kong, China, December 3-7, 2017, Proceedings, Part I, volume 10624 of Lecture Notes in Computer Science, pages 65–95. Springer, 2017.
[Wie83] Stephen Wiesner. Conjugate coding. SIGACT News, 15(1):78–88, 1983.
[Zha19a] Mark Zhandry. How to record quantum queries, and applications to quantum indifferentiability. In Alexandra Boldyreva and Daniele Micciancio, editors, Advances in Cryptology - CRYPTO 2019 - 39th Annual International Cryptology Conference, Santa Barbara, CA, USA, August 18-22, 2019, Proceedings, Part II, volume 11693 of Lecture Notes in Computer Science, pages 239–268. Springer, 2019.
[Zha19b] Mark Zhandry. Quantum lightning never strikes the same state twice. In Yuval Ishai and Vincent Rijmen, editors, Advances in Cryptology - EUROCRYPT 2019 - 38th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Darmstadt, Germany, May 19-23, 2019, Proceedings, Part III, volume 11478 of Lecture Notes in Computer Science, pages 408–438. Springer, 2019.
A A Reduction Between Unclonability Definitions
A.1 In the CRS model
For completeness, here we repeat the definitions of unclonability.
Definition A.1. (Unclonable Security for Hard Instances). A proof (Setup, Prove,Verify) satisfies unclonable security if for every language L with corresponding relation RL, for every polynomialsized quantum circuit family {Cλ}λ∈N, and for every hard distribution {Xλ,Wλ}λ∈N over RL, there exists a negligible function negl(·) such that for every λ ∈ N,

Definition A.2. (1-to-2 Unclonable Extractability) A proof (Setup, Prove,Verify) satisfies unclonable security there exists a QPT extractor E which is an oracle-aided circuit such that for every language L with corresponding relation RL and for every non-uniform polynomial-time quantum adversary A, for every instance-witness pair (x, w) ∈ RL and λ = λ(|x|), such that there is a polynomial p(·) satisfying:
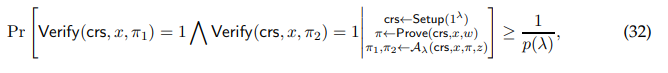
there is also a polynomial q(·) such that
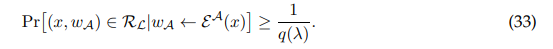
Claim A.3. Any protocol satisfying Definition A.2 also satisfies Definition A.1.
Proof. Suppose there exists a protocol Π = (Setup, Prove, Verify) satisfying Definition A.2.

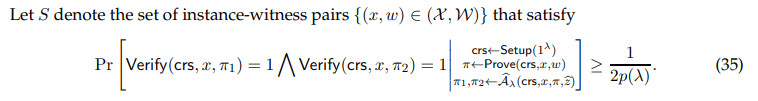

Consider the extractor E guaranteed by Definition A.2. Given a sample (x, w) ← (X ,W), we will show that there is a polynomial p ′ (·) such that
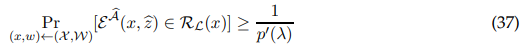
which suffices to contradict hardness of the distribution (X ,W), as desired.
Towards showing that Equation (37) holds, recall by Definition A.2 that for every NP instance-witness pair (x, w) such that there is a polynomial p(·) satisfying:
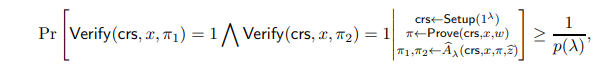
there is also a polynomial q(·) such that
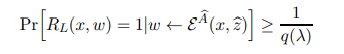
This implies that there is a polynomial q(·) such that for every (x, w) ∈ S,
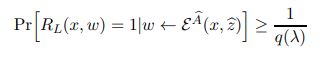
This, combined with Equation (36) implies that
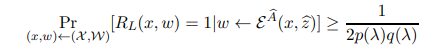
which proves Equation (37) as desired.
A.2 In the QRO model
For completeness, here we repeat the definitions of unclonability.
Definition A.4. (Unclonable Security for Hard Instances). A proof (Prove, Verify) satisfies unclonable security with respect to a quantum random oracle O if for every language L with corresponding relation RL, for every polynomial-sized quantum oracle-aided circuit family {Cλ}λ∈N, and for every hard distribution {Xλ,Wλ}λ∈N over RL, there exists a negligible function negl(·) such that for every λ ∈ N,

Definition A.5. (1-to-2 Unclonable Extractability) A proof (Prove, Verify) satisfies unclonable security with respect to a quantum random oracle O there exists a QPT extractor E which is an oracle-aided circuit such that for every language L with corresponding relation RL and for every non-uniform polynomial-time quantum adversary A, for every instance-witness pair (x, w) ∈ RL and λ = λ(|x|), such that there is a polynomial p(·) satisfying:
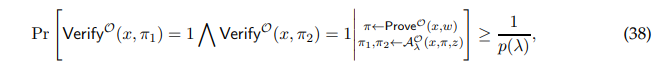
there is also a polynomial q(·) such that
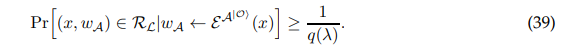
Claim A.6. Any protocol satisfying Definition A.5 also satisfies Definition A.4.
Proof. Suppose there exists a protocol Π = (Prove,Verify) satisfying Definition A.5.
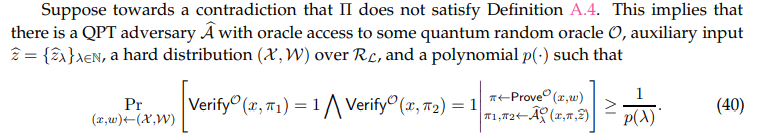
Let S denote the set of instance-witness pairs {(x, w) ∈ (X ,W)} that satisfy
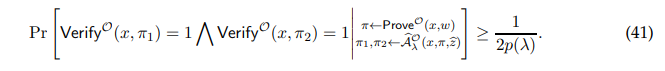
First, we claim that
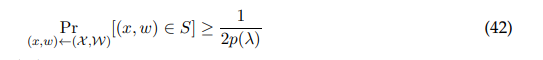
Suppose not, then by Equation (41),
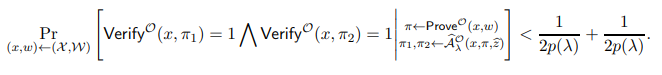
contradicting Equation (40). Thus, Equation (42) must be true.
Consider the extractor E guaranteed by Definition A.5. Given a sample (x, w) ← (X ,W), we will show that there is a polynomial p ′ (·) such that
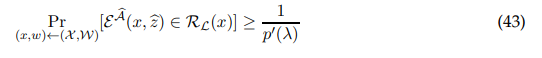
which suffices to contradict hardness of the distribution (X ,W), as desired.
Towards showing that Equation (43) holds, recall by Definition A.5 that for every NP instance-witness pair (x, w) such that there is a polynomial p(·) satisfying:
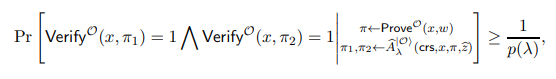
there is also a polynomial q(·) such that
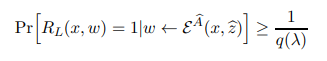
This along with Equation (40) implies that there is a polynomial q(·) such that for every (x, w) ∈ S,
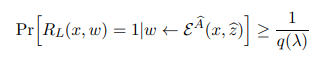
This, combined with Equation (42) implies that
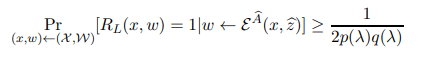
which proves Equation (43) as desired.

