Table of Links
-
The Soup Kitchen Problem
-
Multi-Unit Posted-Price Mechanisms
A. Proofs for Section 2 (The Soup Kitchen Problem)
B. Proofs for Section 3 (Multi-Unit Posted-Price Mechanisms)
4 Transaction fee mechanism design
We take a closer look at the application of our results to designing transaction fee mechanisms, which are used in blockchain technology to allocate limited space on a block.
As discussed in the introduction, space in a block is considered a valuable resource since each block can accommodate only so many units of data (or gas, in the case of Ethereum). A transaction fee mechanism is deployed to decide the inclusion of transactions in a block. Ethereum, for instance, runs a posted-price mechanism that burns all the payments collected from users (Roughgarden, 2020). Conditioned on demand at the price being smaller than capacity of the block, the posted-price mechanism is strategy-proof for users and block proposers, while also deterring collusion between users and block proposers. However, when demand exceeds capacity, an emergency mechanism is deployed wherein the three incentive properties satisfied by the posted-price mechanism cannot all be satisfied simultaneously. The first price auction used by Ethereum as the emergency mechanism is not strategy-proof for users.
Having a high availability is desirable since it corresponds to not needing to frequently deploy the emergency mechanism. However, high availability trades off against throughput. With Bitcoin, where block capacity is an exogenous constraint and absolute throughput is a decision variable, high throughput corresponds to an efficient utilization of the valuable block space. Meanwhile with Ethereum, where absolute throughput is an exogenous constraint and block capacity is a decision variable, high throughput corresponds to low block capacity, and thereby, a smaller amount of information to process for block proposers in periods of high demand.
An ideal price-adjustment mechanism would like to directly control for availability. However, measuring availability is not straightforward since whether the demand exceeds the capacity of a block is binary; either the demand exceeds capacity, or it does not. Instead, price-posting heuristics use throughput and absolute throughput as an easily measurable lever to indirectly ensure high availability. Ethereum targets maintaining an average absolute throughput of 15 million gas, and achieves this through a heuristic that increases (decreases) the price if the ex-post absolute throughput of the previous block was more (less) than the 15 million gas target. Ethereum supports up to 30 million gas in each block, and thus, the heuristic translates to maintaining a 50% throughput. Improved methods for managing this tradeoff have been proposed (Ferreira et al., 2021).
Our analysis of the shape of the tradeoff curve suggests a scope to reduce the block capacity (and thus, increase the throughput) without a significant decrease in availability[2]. The target absolute throughput is 15 million gas, while 750,000 is a conservative upper bound on the maximum gas requested by any single transaction. Thus, the effective supply is at least 40. Targeting a 50% throughput would guarantee an availability of at least 99.9%. On the other hand, for a reduced supply of 26.25 million gas (corresponding to an effective supply of 35), a target absolute throughput of 15 million gas would correspond to a 57% throughput. Our bounds on availability, given this smaller effective supply and larger throughput target, would guarantee an availability of at least 99.7%, which is only a minor decrease from the status quo.
For the parameters mentioned in the previous paragraph, we can also examine the case where block capacity is exogenously fixed and the absolute throughput is a decision variable (like in Bitcoin). Figure 7 plots the availability vs throughput tradeoff for κ = 40, using an optimal ReLU bound from Theorem 3. It is possible to select different points along the tradeoff curve using different throughput targets. For minor sacrifice in availability, a significant gain in throughput can be realized. For instance, a throughput of 60% guarantees an availability of at least 99.66%, which translates to requiring the emergency auction approximately once every 300 blocks. A throughput of 60% would also guarantee approximately 60% of the optimal welfare (Proposition 4). As with Ethereum, this is a only minor decrease in availability from the status quo.
5 Conclusions and future work
For posted-price mechanisms, we are able to significantly improve upon the lower bounds on expected welfare provided by a conventional Chernoff bound. Our bounds on throughput in terms of availability also improve on the analytical tractability of those provided by Chawla, Devanur, and Lykouris (2023) without significantly sacrificing strength, and can be applied to settings with up-to-unit-demand agents.
We are able to show that the unavailability δ can be made much smaller than its usual value in prophet inequalities, with only a minor penalty to expected welfare. As can be seen from Figure 4
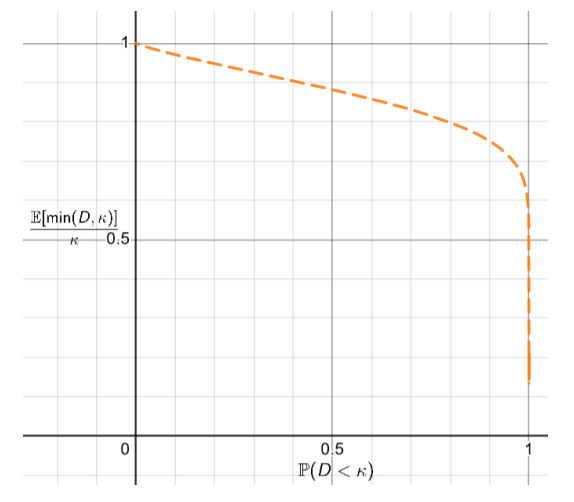
and Figure 6, several of our derived lower bounds on throughput τ are nearly flat as a function of δ near the peak of the welfare curve. A nearly flat curve suggests that prices intentionally selected to be higher than their welfare-optimal value can significantly decrease unavailability δ with only a minor impact on throughput τ , and thus only a minor impact on expected welfare. A mechanism designer has good reason to make δ as small as possible, and so may wish to take advantage of this favorable tradeoff.
The bounds we derive can almost certainly be made tighter, and this is an important area for future work. Chawla, Devanur, and Lykouris (2023) are able to demonstrate that Poisson-distributed demand produces the worst ratio of expected welfare achieved by a posted-price mechanism compared to a prophet in a unit-demand setting. In comparison, as can be seen from Figure 4, the throughput τ corresponding to a true Poisson distribution for any given availability α is above the strongest lower bounds on τ available from Theorem 3, via selecting an optimal ReLU function. The tradeoff curve for Poisson distributions would need to be identical to the strongest bound from Theorem 3 for the proof techniques demonstrated in this paper to extend the results of Chawla, Devanur, and Lykouris (2023) that Poisson demand is worst-case from the unit-demand setting to the up-to-unit-demand setting. Future work should seek to close the gap between the two tradeoff curves.
Another area for future work is to refine our availability-throughput bounds to better capture salient features of the demand distribution in Ethereum blocks. The concentration inequalities presented in this paper assume only that individual demands are independent and up-to-unit, and if stronger assumptions can be made on the individual demands’ distributions, stronger concentration inequalities could be developed. For example, in Ethereum it is known that the gas requested by many transactions falls below their maximum possible value. Our analysis used a conservative upper bound on the gas requested by any single transaction of 750, 000. However, a standard transfer between two Ethereum wallets requires 21, 000 units of gas, which is an order of magnitude smaller. Since the variability in the gas requested by each transaction is high, the “effective supply” of κ = 40 that we selected is an underestimate; most blocks typically accommodate over 100 transactions. A more refined analysis that takes into account these empirical facts could demonstrate an improved tradeoff between throughput and availability, by restricting attention to more realistic demand distributions rather than the worst-case demand distributions examined in this paper.
References
Hoeffding, Wassily (1956). “On the distribution of the number of successes in independent trials”. In: The Annals of Mathematical Statistics, pp. 713–721.
Suzuki, Yoshinori (2002). “An empirical analysis of the optimal overbooking policies for US major airlines”. In: Transportation Research Part E: Logistics and Transportation Review 38.2, pp. 135–149.
Goldberg, Andrew V and Jason D Hartline (2003). “Envy-free auctions for digital goods”. In: Proceedings of the 4th ACM conference on Electronic commerce, pp. 29–35.
Bertsimas, Dimitris and Sanne De Boer (2005). “Simulation-based booking limits for airline revenue management”. In: Operations Research 53.1, pp. 90–106.
Hajiaghayi, Mohammad Taghi, Robert Kleinberg, and Tuomas Sandholm (2007). “Automated online mechanism design and prophet inequalities”. In: AAAI. Vol. 7, pp. 58–65.
Lee, Gunho and Randy H Katz (2011). “Heterogeneity-Aware Resource Allocation and Scheduling in the Cloud”. In: 3rd USENIX Workshop on Hot Topics in Cloud Computing (HotCloud 11).
Buterin, Vitalik et al. (2014). “A next-generation smart contract and decentralized application platform”. In: white paper 3.37, pp. 2–1.
Boyd, E (2016). The future of pricing: How airline ticket pricing has inspired a revolution. Springer.
Lu, Qiumin et al. (2016). “Fairness-efficiency allocation of CPU-GPU heterogeneous resources”. In: IEEE Transactions on Services Computing 12.3, pp. 474–488.
Jeon, Myeongjae et al. (2018). “Multi-tenant GPU clusters for deep learning workloads: Analysis and implications”. In: Technical report, Microsoft Research.
Roig-Solvas, Biel and Mario Sznaier (2020). “Euclidean Distance Bounds for LMI Analytic Centers using a Novel Bound on the Lambert Function”. In: arXiv preprint arXiv:2004.01115.
Roughgarden, Tim (2020). “Transaction fee mechanism design for the Ethereum blockchain: An economic analysis of EIP-1559”. In: arXiv preprint arXiv:2012.00854.
Ferreira, Matheus VX et al. (2021). “Dynamic posted-price mechanisms for the blockchain transactionfee market”. In: Proceedings of the 3rd ACM Conference on Advances in Financial Technologies, pp. 86–99.
Roughgarden, Tim (2021). “Transaction fee mechanism design”. In: ACM SIGecom Exchanges 19.1, pp. 52–55.
Liu, Yulin et al. (2022). “Empirical analysis of eip-1559: Transaction fees, waiting times, and consensus security”. In: Proceedings of the 2022 ACM SIGSAC Conference on Computer and Communications Security, pp. 2099–2113.
Arnosti, Nick and Will Ma (2023). “Tight guarantees for static threshold policies in the prophet secretary problem”. In: Operations research 71.5, pp. 1777–1788.
Chawla, Shuchi, Nikhil Devanur, and Thodoris Lykouris (2023). “Static pricing for multi-unit prophet inequalities”. In: Operations Research.
Chung, Hao and Elaine Shi (2023). “Foundations of transaction fee mechanism design”. In: Proceedings of the 2023 Annual ACM-SIAM Symposium on Discrete Algorithms (SODA). SIAM, pp. 3856–3899.
Jiang, Jiashuo, Will Ma, and Jiawei Zhang (2023). “Tightness without Counterexamples: A New Approach and New Results for Prophet Inequalities”. In: Proceedings of the 24th ACM Conference on Economics and Computation. EC ’23. , London, United Kingdom, Association for Computing Machinery, p. 909. isbn: 9798400701047. doi: 10.1145/3580507.3597734. url: https://doi.org/10.1145/3580507.3597734.
Chung, Hao, Tim Roughgarden, and Elaine Shi (2024). “Collusion-resilience in transaction fee mechanism design”. In: arXiv preprint arXiv:2402.09321.
A Proofs for Section 2 (The Soup Kitchen Problem)

Proof. Proving Theorem 1 can be split into the above two separate steps. The first of these two steps is Lemma 2, proved subsequently. Consider that when we select L = 0, Lemma 2 tells us that
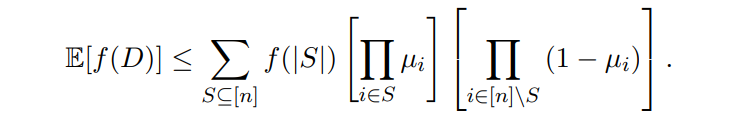
for µ1, ..., µn denoting the means of the individual random variables D1,...,Dn.
Observe that Lemma 3 also allows us to show
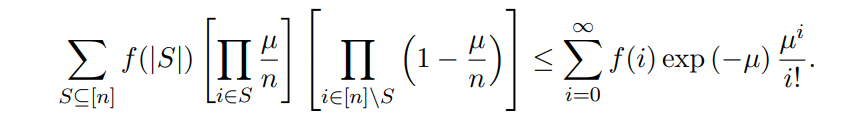
To see this, let n ′ ≫ n and begin with µi = µ/n for all i ∈ [n] and µi = 0 for all i ∈ [n′] \ [n].
Then, the procedure laid out in Lemma 3 lays out a path by which all µi converge to µ/n′ and demonstrates
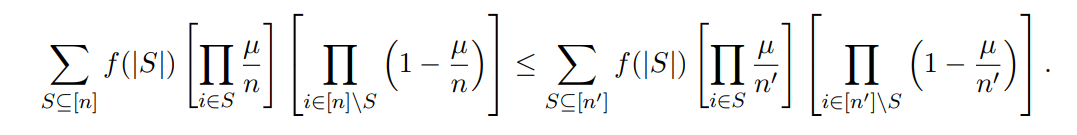
Furthermore, observe that by the definition of a binomial distribution,
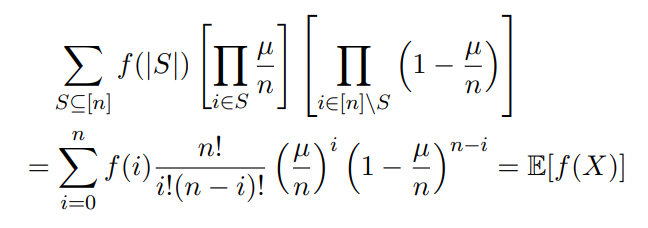
for X ∼ Binomial(n, µ/n). Therefore, as we’ve demonstrated that E[f(X)] is weakly increasing in n, we have E[f(X)] ≤ E[f(Y )] for Y ∼ Poisson(µ), which is the limiting case as n → ∞. We conclude that Theorem 1 must hold, i.e. for our initial random variable D that is the sum of n independent Di ∈ [0, 1],
E[f(D)] ≤ E[f(X)] ≤ Y)].

Proof. We first introduce some notation. Let µ ≜ E[D], and denote the upper conditional mean µ↑ ≜ E[D | D ≥ κ] and the quantity µ↓ ≜ E[D1(D < κ)]; thus, µ = µ↑P(D ≥ κ) + µ↓.
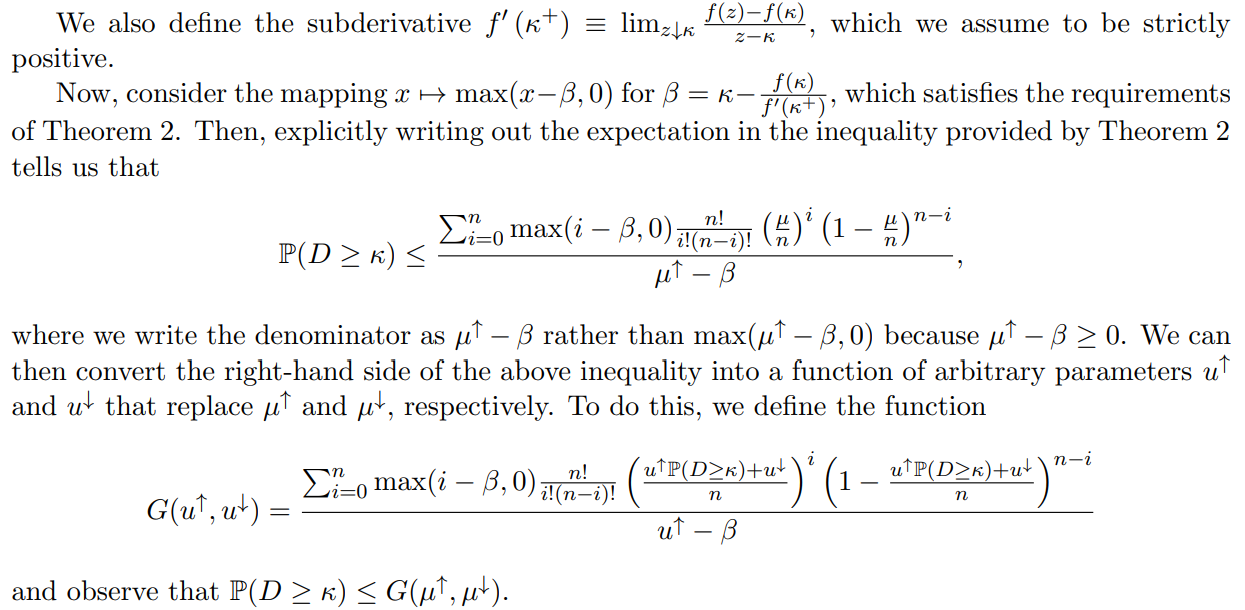
We will manipulate the parameters of this function G to show that G(µ↑, µ↓) ≤ G(κ, µ↓), allowing us to conclude that P(D ≥ κ) ≤ G(κ, µ↓). To do this, we will examine two cases: where β ≥ 0, and where β < 0. In the case where β ≥ 0, we will first showcase a continuous path in (u↑, u↓) space that preserves the value of G and goes from (µ↑, µ↓) to (κ, t) for some t ≤ µ ↓. Then, we will apply the fact that G(κ, ·) is weakly increasing to show G(µ↑, µ↓) ≤ G(κ, µ↓). In the case where β < 0, we will instead show directly that G(·, µ↓) is decreasing.
Assume that β ≥ 0. Observe that for any fixed u ↑ ∈ (β, µ↑], the function G(u↑, ·) is continuous across all inputs u ↓ such that
u↑P(D ≥ κ) + u ↓ ∈ [0, n].
In other words, G(u↑, ·) is continuous in the closed interval [−u ↑P(D ≥ κ), n − u ↑P(D ≥ κ)
Note that the value u ↓ = (µ↑ − u↑)P(D ≥ κ) + µ↓ lies in this interval, which we briefly verify by checking th
u↑P(D ≥ κ) + (µ↑ − u↑)P(D ≥ κ) + µ↓ = µ↑ P(D ≥ κ) + µ
= µ ≜ E[D] ∈ [0, n
It follows that since G(u↑, ·) is continuous in the interval [−u↑P(D ≥ κ), n − u ↑P(D ≥ κ)], it is also continuous in the subinterval [−u↑P(D ≥ κ),(µ ↑ − u↑)P(D ≥ κ) + µ↓]
We now observe that when u ↓ is equal to the endpoints of this interval, −u↑P(D ≥ κ) and (µ↑−u ↑)P(D ≥ κ)+µ ↓, we obtain values of G that are lower and higher than G(µ ↑ , µ↓ ), respectively
First, when u ↓ = −u↑P(D ≥ κ), we have
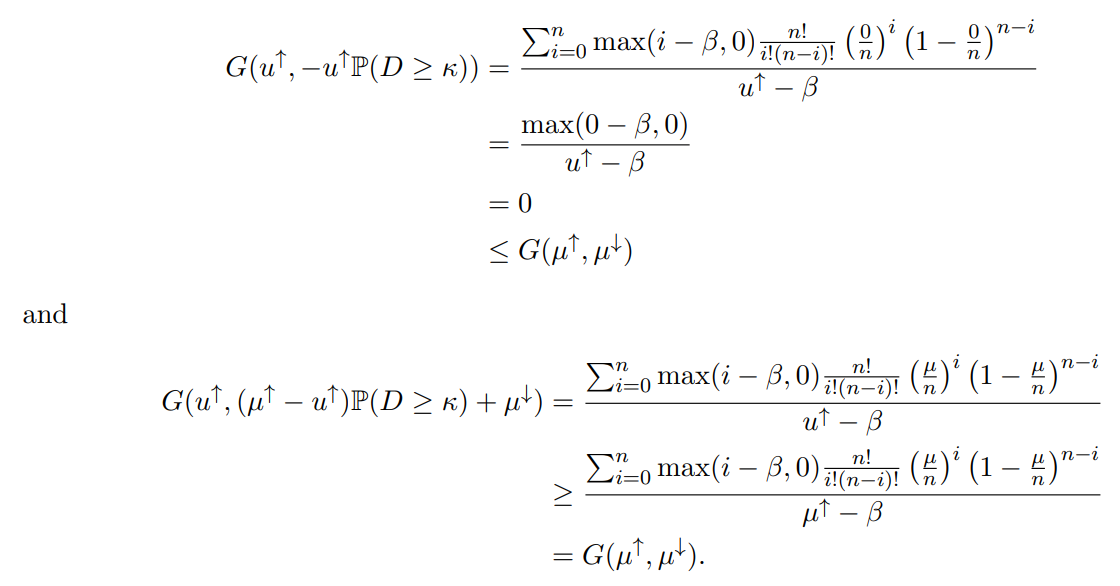
Therefore, by the intermediate value theorem, there will always exist some u ↓ within the interval [−u ↑P(D ≥ κ),(µ↑ − u↑)P(D ≥ κ) + µ↓] such that G(u↑, u↓) exactly equals G(µ↑, µ↓). We will hereafter write u ↓ as a function of u ↑ so as to always select a u ↓ where this equality
G(u↑, u↓ (u↑)) = G(µ↑ ,µ↑)
By definition, varying u↑ keeps the left-hand side of the above equality constant. Thus, if we take the total derivative of G with respect to u↑, we will always have
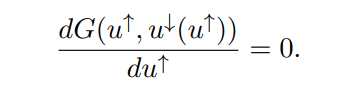
We will use this fact to demonstrate that u↓ (u↑) is weakly increasing in u↑. To do so, we compute the total derivative as folows:
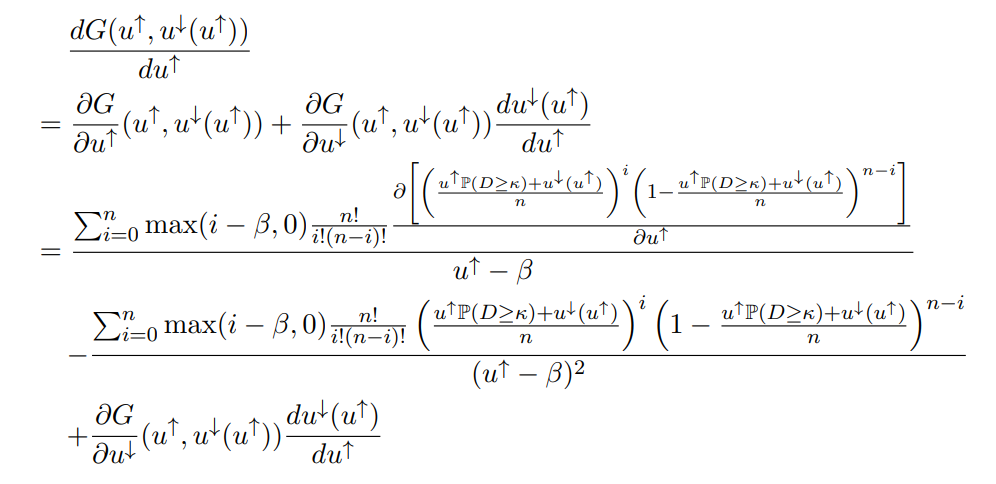
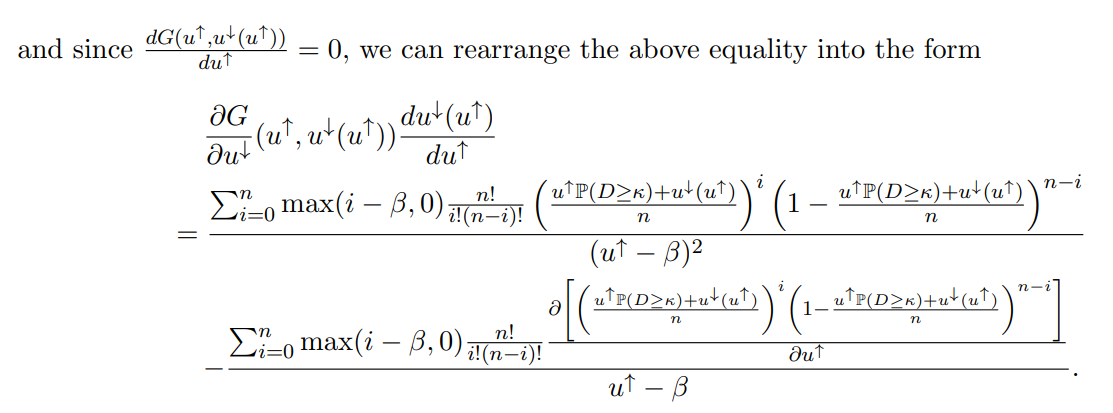
Observe that the two terms on the right-hand side can be simplified, respectively, as
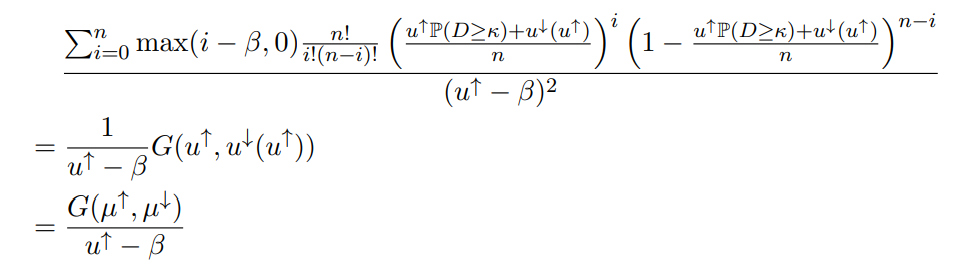
and

Thus, we have
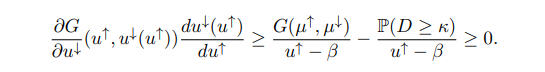
Lastly, note that G(u↑, ·) is a weakly increasing function, as the numerator of

lets us conclude that
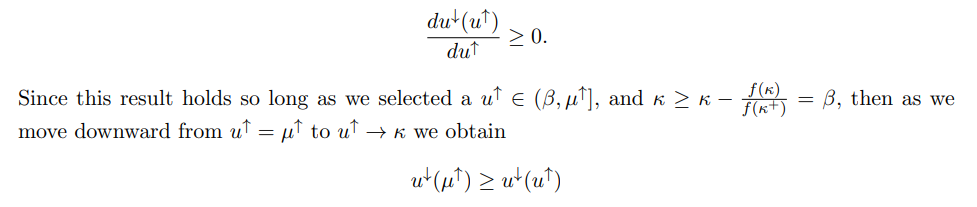
for all u↑ ∈ (κ, µ↑]. Recall additionally that u↓ (u↑) ∈ [−u ↑P(D ≥ κ), (µ↑ − u↑)P(D ≥ κ) + µ↓], which provides an upper bound on u↓ (µ↑):
u↓ (µ↑) ≤ (µ↑ − µ↑)P(D ≥ κ) + µ↓ = µ↓
Hence, u↓ (u↑) ≤ µ ↓ for all u ↑ ∈ (κ, µ↑]. Furthermore, from the facts that G(u ↑, u↓ (u ↑)) = G(µ , µ↓) for all u ↑ ∈ (κ, µ↑] and that G(u↑, ·) is weakly increasing, we can deduce that
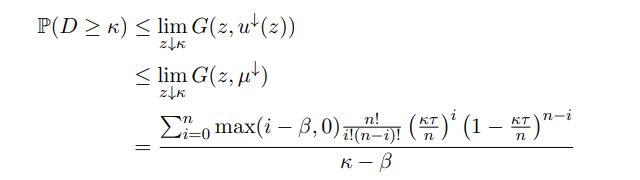
with the bound becoming infinitely weak when κ = β and τ > 0. We can observe that the righthand side can be written as an expectation with respect to a binomial distribution with mean κτ , and so we have
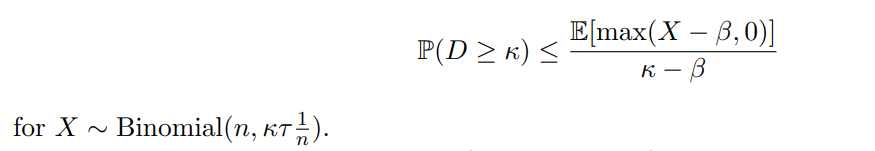
We now examine the case where β<0. Let us fix the parameter u↓ = µ↓ and observe what happens as we vary the parameter u↑. We first note that since µ↓ ≥ 0, the inequalities
µ ≥ u↑P(D ≥ κ) + µ↓ ≥
hold for any u↑ ∈ [0, µ↑], and so the summation
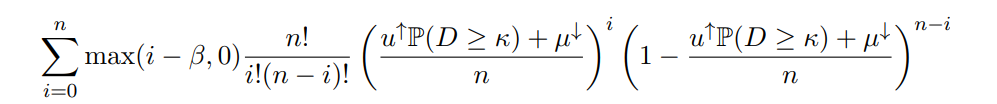
in the numerator of G(u↑, µ↓) is an expectation of max(i − β, 0) with respect to a binomial distribution with mean u↑ P(D ≥ κ) + µ↓. Additionally, if β < 0, then max(i − β, 0) = i − β for all i ∈ {0,1, ..., n}. Thus, we compute that
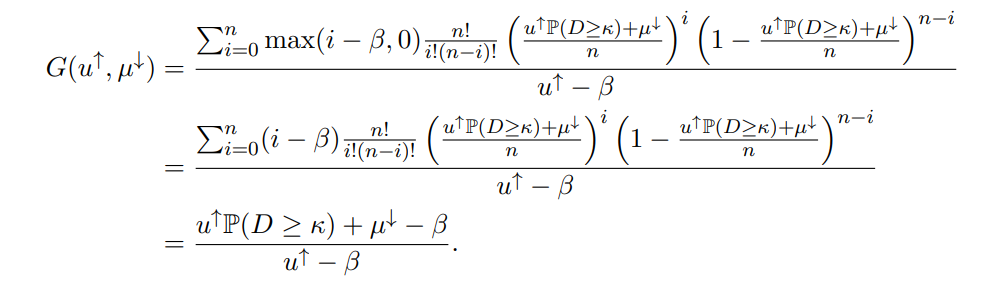
Taking the partial derivative of G with respect to u↑, we obtain

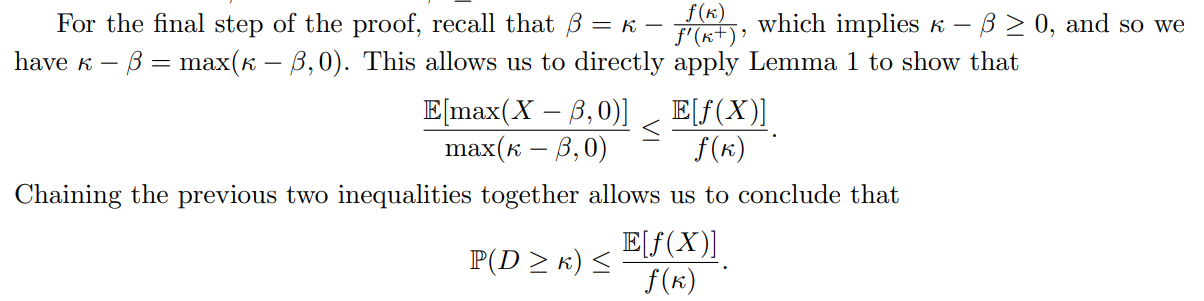








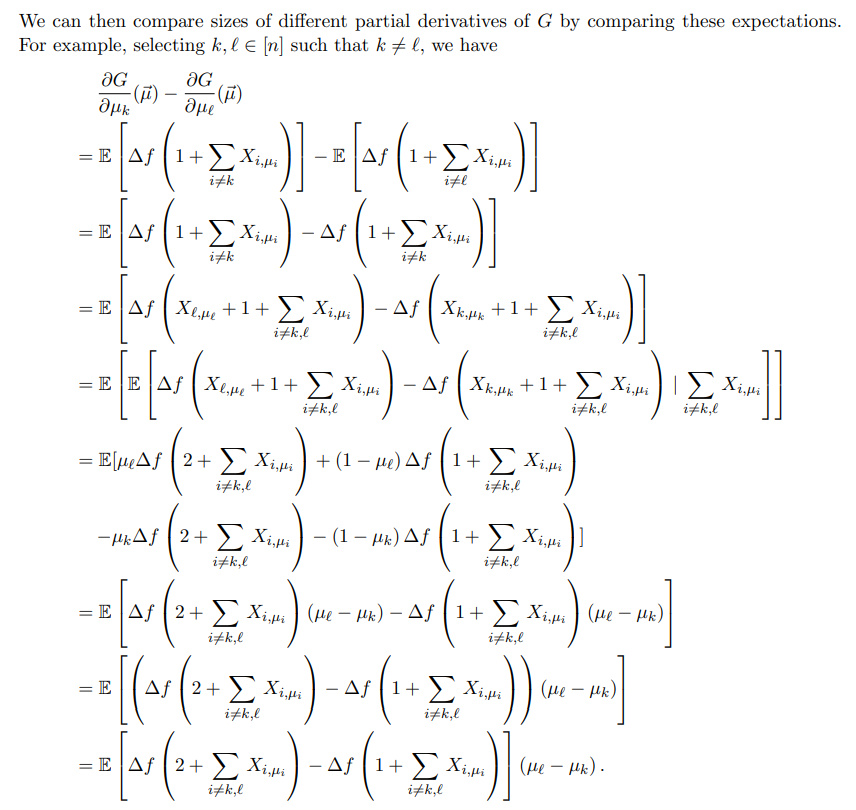



B Proofs for Section 3 (Multi-Unit Posted-Price Mechanisms)
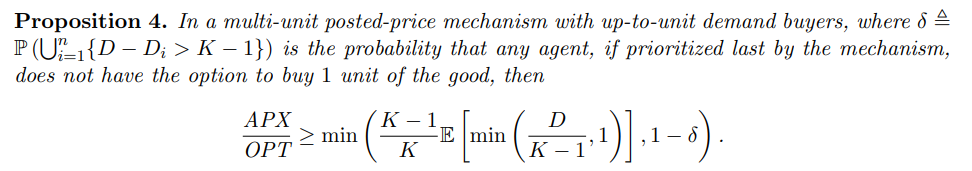

with the last step following from the fact that agents, no matter how much is left on the shelf when they arrive at the mechanism, can always choose to buy nothing at all and obtain 0 utility. More formally,
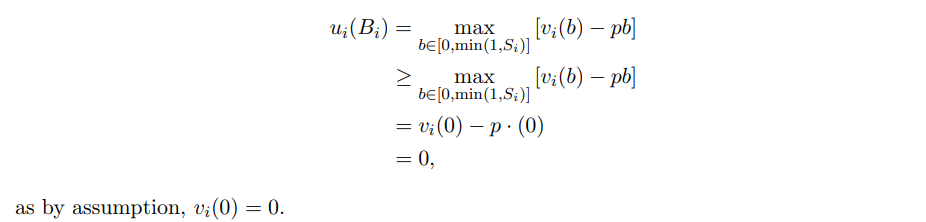


We will now proceed to upper bound OPT. We compute as follows:
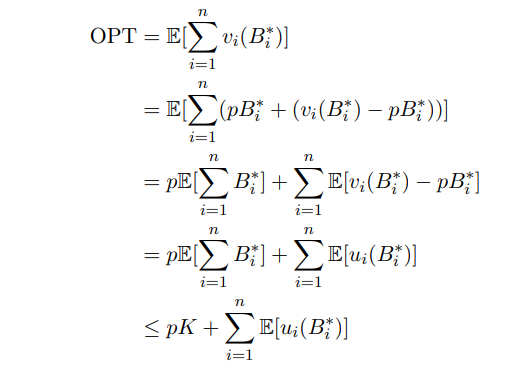
The last step follows from the fact that no allocation, including the optimal allocation, can use more than the total stock of K goods.
Combining our lower and upper bounds for APX and OPT, respectively, we have
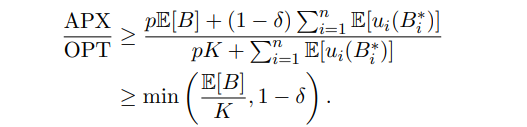
This splits our welfare bound into two cases; a high δ case, where the term 1 − δ is smaller, and a low δ case, where the term E[B]/K is smaller.
Our goal now becomes finding a lower bound for E[B]/K in terms of D. We begin by applying the law of total expectation to E[B], yielding
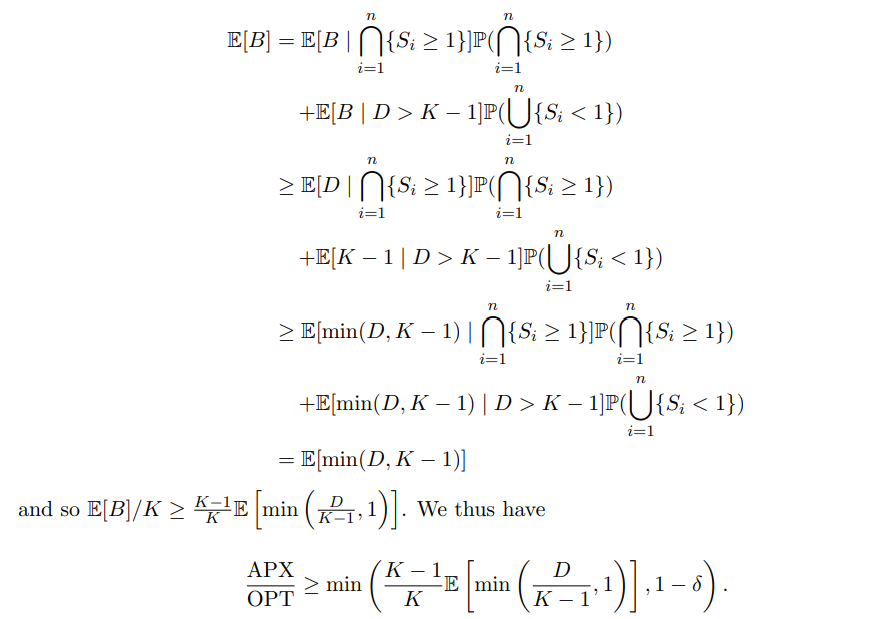

Multiplying both sides by exp(λκ) − 1 and adding 1 to both sides, and we obtain
δ exp(λκ) + (1 − δ) ≤ E[exp(λY )].
Using the formula for the moment-generating function of a Poisson-distributed variable, we have E[exp(λY )] = exp(κτ (exp(λ) − 1)). Inserting this into the above inequality and rearranging gives us
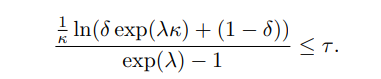
This bound holds for any positive λ, but would be stronger for some selections of λ than others. The optimal λ does not have a closed form, but it can be very closely approximated. Consider that
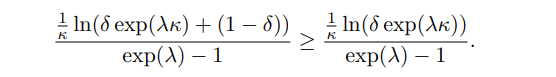
Close approximations to the optimal λ on the right-hand side will tend to be underestimates of the optimal λ on the left-hand side. Thus, we will demonstrate a bound on the optimal λ for the left-hand side. We begin by taking the first derivative with respect to λ and setting it equal to 0:
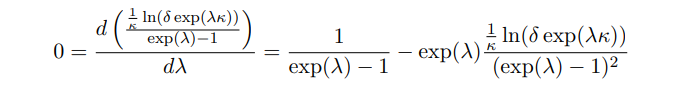
Rearranging gives us
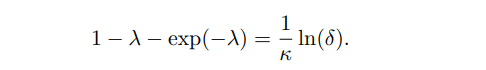

Authors:
(1) Aadityan Ganesh, Princeton University ([email protected]);
(2) Jason Hartline, Northwestern University ([email protected]);
(3) Atanu R Sinha, Adobe Research ([email protected]);
(4) Matthew vonAllmen, Northwestern University ([email protected]).
This paper is
[2] In practice, the likely effects on availability are less clear. In Ethereum, the emergency auction is triggered in around 2.3% of blocks (Chung, Roughgarden, and Shi, 2024; Liu et al., 2022), corresponding to 97.7% availability. This is lower than what our tradeoff curves would permit if throughput were fixed to 1/2, and suggests that Ethereum’s price adjustment to maintain its 1/2 throughput target is not fast enough. When the price lags behind its ideal level, blocks may achieve a throughput either far above or below the 1/2 target, and it is the average availability between these two cases which produces the 97.7% figure.

