Table of Links
C. Comparison with Related Works
II. Background
C. Assumptions and Approximations
IV. Results
V. Discussion, Acknowledgments, and References
C. Example Application
In this subsection we demonstrate an application of our results by calculating numerical estimates for a quantum miner’s performance. These calculation demonstrate how to use our results to evaluate the feasibility of a given quantum computer for Bitcoin mining. We give estimates for both effective hash rate and energy efficiency required for advantegous mining.
The quantum computer we consider is described in [4]. First, the computer has a gate speed of 66.7 MHz, which is the speed achievable on current devices. Aggarwal et al. also show that a single Grover iteration (for the Bitcoin search problem) would take a circuit of depth 297784 to perform if we assume no overhead from error correction. We make this assumption for simplicity as the error correction overhead has a non-trivial relationship with the number of sequential Grover iterations used. For this quantum computer,


This means the quantum computer would comprise only a small fraction of the mining power of the Bitcoin network. Finally, we calculate the effective hash rate to be

Efficiency Requirement Next we turn to the efficiency the quantum computer would need to outperform a classical computer at Bitcoin mining. Recall the condition for this outperformance is given by Eq. 63. Plugging into this equation we find the condition
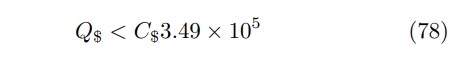
for advantageous quantum mining. If we instead use Eq. 69 which employs an additional approximation, then we get same result, up to three significant figures.

Authors:
(1) Robert R. Nerem, Institute for Quantum Science and Technology, University of Calgary, Alberta T2N 1N4, Canada ([email protected]);
(2) Daya R. Gaur, Department of Mathematics and Computer Science, University of Lethbridge, Alberta T1K 3M4, Canada.
This paper is

