Zero Knowledge Proof based Gradient Aggregation for Federated Learning: Theoretical Analysis

TABLE OF LINKS

Abstract & Introduction

Related Work & Preliminaries

Methodology

Theoretical and Empirical Analysis

Results

Conclusion & References

Theoretical Analysis

In the following, we provide analyses to show that our zkFL and blockchain-based zkFL systems can achieve the goals of security and privacy, while merely bringing an acceptable decrease in the FL training efficiency.

Security Analysis

Our zkFL and blockchain-based zkFL can achieve the security goal through the following techniques:

• The signatures sigi of each encrypted local update Enc(wi) ensure the local updates’ integrity from the clients and prevent the aggregator from tampering with their content and the statement statement = (Enc(w1), sig1, ..., Enc(wn), sign, Enc(w)).
• The completeness and soundness properties of the ZKP proof π play a critical role in safeguarding the aggregation process from adversarial manipulation by the aggregator.

These properties ensure that the aggregator cannot deviate from the intended behaviors:

• If the aggregator abandons the model update generated from one client j, then the aggregated results will be ˆw = Pn i=1,j̸=i wi. In this case, the corresponding circuit C(statement, witness) outputs 0, and the proof π will be invalid.
• If the aggregator replaces the model update generated from one client j by wˆj, then the aggregated results will be ˆw = Pn i=1,j̸=i wi + ˆwj. In this case, the corresponding circuit C(statement, witness) outputs 0, and the proof π will be invalid.
• If the aggregator inserts one fake model update generated ˆw0, then the aggregated results will be ˆw = Pn i=1 wi+ ˆw0. In this case, the corresponding circuit C(statement, witness) outputs 0, and the proof π will be invalid. Therefore, the proof π will only be valid if the aggregator honestly conducts the local model updates aggregation to generate the global model update P w = n i=1 wi.

Privacy Analysis

In zkFL, privacy is inherently ensured as only the aggregator and the participating clients are involved in the training and aggregation process, eliminating the need for external parties. As a result, only these authorized entities possess knowledge of the aggregated model updates at each round. In the context of the blockchain-based zkFL system, the blockchain miners receive encrypted the local model updates Enc(wi) (1 ≤ i ≤ n), the encrypted global model update Enc(w), and the ZKP proof π from the aggregator.

However, due to the zero-knowledge property of ZKP, the miners can only verify whether Enc(w) is correctly executed or not, without gaining any access to information about the individual local model updates wi (1 ≤ i ≤ n) or the global model update w. Additionally, storing the encrypted data of Enc(w) on the blockchain does not compromise the privacy of the global model update w. Our system maintains a robust level of privacy throughout the blockchain-based zkFL process.

Efficiency Analysis

In the following, we calculate the expected computation time of the aggregator and a client per round, to analyze the system efficiency of zkFL and blockchain-based zkFL. In both zkFL and blockchain-based zkFL systems, the aggregator is responsible for aggregating the local model updates and generating the ZKP proof. The expected computation time of the aggregator is:

Eaggregator = E(aggr) + E(ZKP.gen)

In the zkFL system, a client needs to train the local model, encrypt the local model update and verify the ZKP proof generated by the aggregator. The expected computation time of a client is:

Eclient = E(train) + E(enc) + E(ZKP.ver)

In the blockchain-based zkFL system, a client still needs to train the local model and encrypt the local model update. However, the blockchain miners will take charge of verifying the ZKP proof generated by the aggregator, and the clients only need to read the data on the blockchain. The expected computation time of a client is:

E block client = E(train) + E(enc) + O(1)

Empirical Analysis

In this section, we quantify the overhead of zkFL and show that it can be used to train practical FL models.

Experiment Setup

Implementation. We develop a prototype of zkFL. We implement the prototype in Rust and interface it with Python to train deep learning models withPyTorch 1.13. We adopt the elliptic curve Curve25519 (i.e. 126-bit security) implementation from the dalek curve25519 library for cryptographic encryption operations. We build Pedersen commitments [1] over the elliptic curves and integrate it with Halo2 [5], a ZKP system that is being used by the Zcash blockchain.

We test our zkFL system with two families of network architectures: ResNets [13] (ResNet18, ResNet34, ResNet50) and DenseNets [14] (DenseNet121, DenseNet169, and DenseNet201). We use this setup to evaluate the sensitivity of zkFL to network architectures and number of parameters. We use a standard Adam optimizer [20] with fixed learning rate 0.001 with batch size 50. We use the area under the receiver operating curve (AUROC) as the evaluation metric. All tests are implemented in PyTorch 1.10.1 on an NVIDIA Tesla T4 GPU with 16GB memory.

Data and Task

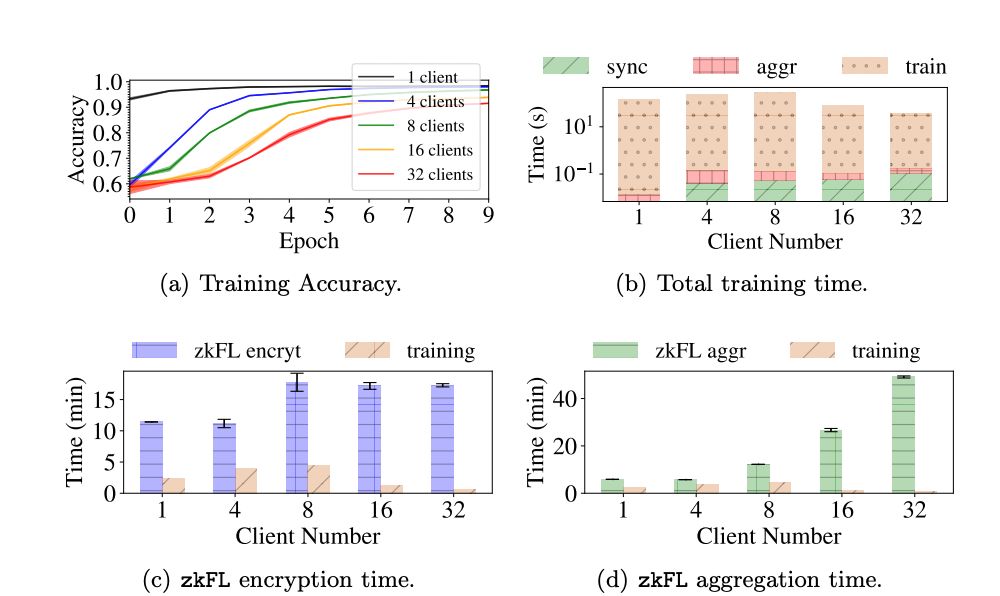
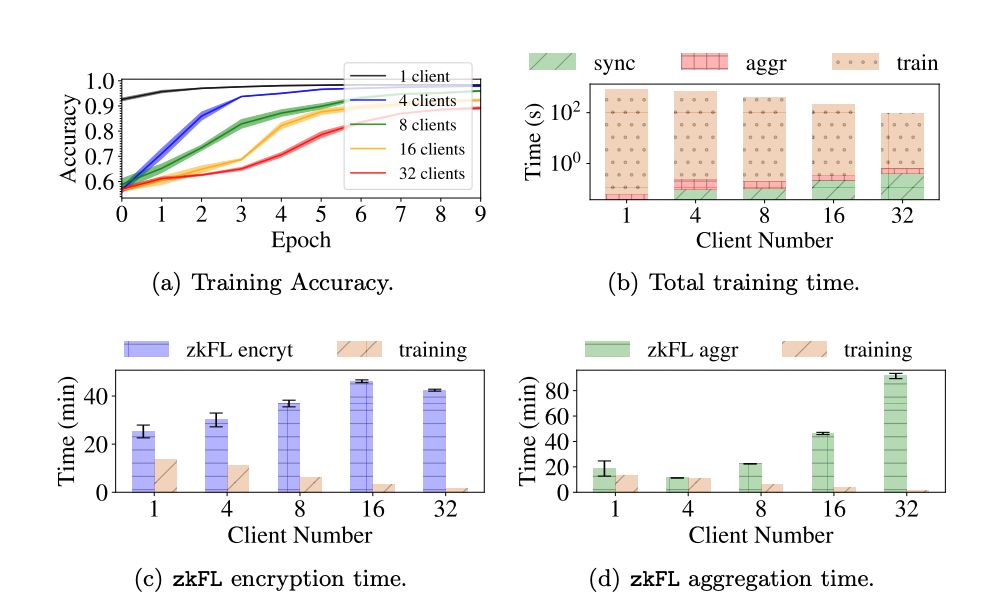
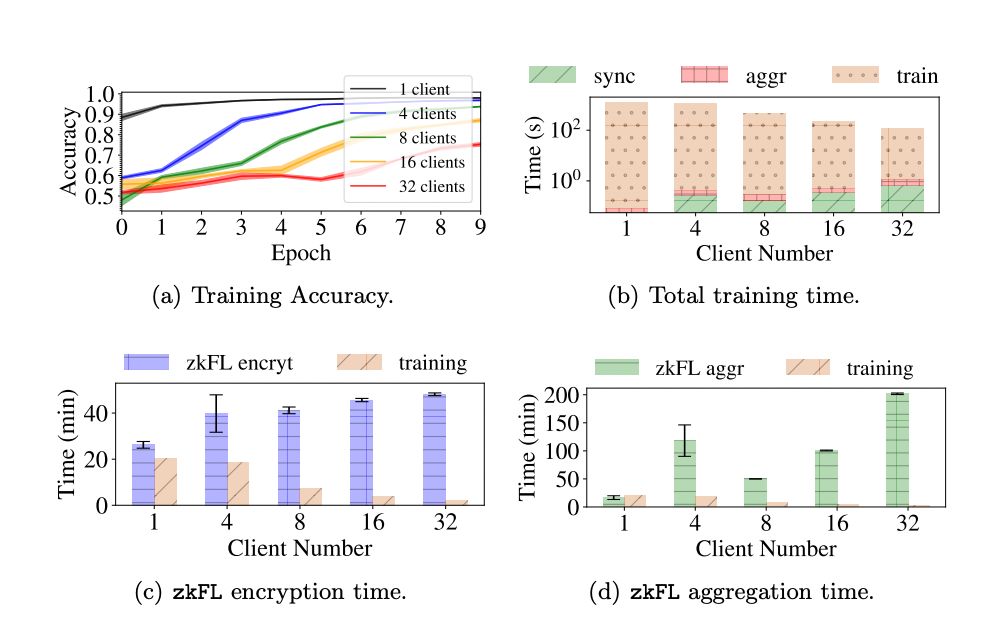
We consider a benchmark classification task under the common federated setup. We use FedAVG [23] as the base FL method to evaluate zkFL and use CIFAR-10 dataset with the default train-test split. The training set is split into K subsets of equal size and distributed across K clients. For each client, 10% of distributed data is assigned as the validation set. In each epoch, clients train their models separately with local data. Then, the aggregator synchronizes local models and performs the model evaluation. For each network backbone, we conduct the tasks for zkFL with 1, 4, 8, 16, and 32 client(s).

For each task, we record the training time without using zkFL, the encryption and aggregation time with zkFL, as well as the ZKP generation and verification time under zkFL. We also evaluate the performance of each task with various network backbones and client numbers.