Table of Links
C. Comparison with Related Works
II. Background
C. Assumptions and Approximations
IV. Results
V. Discussion, Acknowledgments, and References
B. Markov Chain
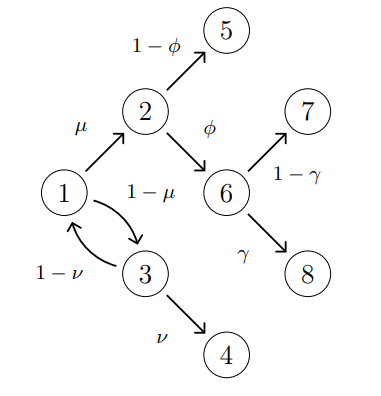
To determine probability of success, we represent the aggressive mining procedure using the state transition graph in Figure 1. If we take φ = 0, then this state transition graph describes the peaceful mining procedure. We define T := K/r where K is the number of Grover iterations and r is the speed of the quantum miner in Grover iterations per second. The executing events in the protocols are as follows.
(1) → (2) Some classical miner announces a valid block before T.
(2) → (6) The quantum miner discovers a valid block using aggressive mining before T.
(2) → (5) The quantum miner fails at aggressive mining, and the classically mined block is accepted to the blockchain.
(1) → (3) No classical miner finds a block before T.
(3) → (4) The quantum miner discovers a valid block at time T.
(3) → (1) The quantum miner’s measurement at time T fails to yield a valid block.
(6) → (7) The classically mined block gets accepted and the quantum miner’s block becomes stale.
(6) → (8) The quantum miner’s block gets accepted and the quantum miner’s block becomes stale.
We model these events as independent, and their probabilities are in the KEY. Quantum miner generate a valid block in two situations.
(4) No classical miner finds a block in time T (probability 1 − µ), and the quantum miner’s subsequent measurement succeeds, which occurs with probability ν.
(8) Some classical miner generates a valid block before T with probability µ and announces the block to the network. The quantum miner receives this valid block, and in response, performs a measurement (aggressive mining) that succeeds with probability φ. Subsequent blocks are then added to on top of the quantum miner’s block, as opposed to the classical miner’s block resulting in acceptance of the quantum miner’s block(probability γ).

KEY
-
Initial state
-
Classical miner has found a block in time T (ln 5)
-
Classical miner did not find a block in time T (ln 19)
-
Quantum miner finds a block (ln 21)
-
In response to classical miner finding a block, the quantum miner measured and failed to find a block (ln 15)
-
In response to classical miner finding a block, the quantum miner measured and found a block (ln 11)
-
Classical miner’s block is accepted
-
Quantum miner’s block is accepted
(ν) Probability the quantum miner’s measurement after T seconds of Grover iterations yields a block to the quantum miner
(µ) Probability the classical miner finds a block before T
(φ) Quantum miner finds a block in response to classical miner finding a block first (aggressive mining)
(γ) Fraction of miners who mine on the quantum miner’s block when a fork occurs
States (4), (5), (7), (8) contain self loops of weight 1 (not shown)
FIG. 1. State transition graph for quantum Bitcoin mining.
Our procedure assumes a K that is not changed between iterations. However, the constant K case always contains an optimal quantum mining procedure; as the state of the system directly after a failed quantum measurement is always identical, a value of K that maximizes the quantum miner’s future success following this measurement must also be the same as the initial choice for K. In short, as each time the quantum miner reaches (1), the state of the system is indistinguishable, the quantum miner can always make the same choice of K.
Authors:
(1) Robert R. Nerem, Institute for Quantum Science and Technology, University of Calgary, Alberta T2N 1N4, Canada ([email protected]);
(2) Daya R. Gaur, Department of Mathematics and Computer Science, University of Lethbridge, Alberta T1K 3M4, Canada.
This paper is

