Table of Links
-
Protocol
-
Security Analysis
A. Codes
B. Proofs
4.2 Holder Collateral-Free Cross-Chain Options
We want to remove the need for upfront collateral from Alice without using a cross-chain bridge. Allowing Alice direct access to the exercise secret risks Bob’s asset since Alice has no collateral. To address this, we resort to economic incentives and let Bob control the exercise secret while Alice retains the right to penalize Bob. In addition to the usual collateral, Bob locks a valuable asset on 𝐶ℎ𝑎𝑖𝑛𝐴 as a guarantee. If Bob fails to release the exercise secret when Alice exercises her right, she receives Bob’s guarantee as compensation, incentivizing Bob to cooperate.
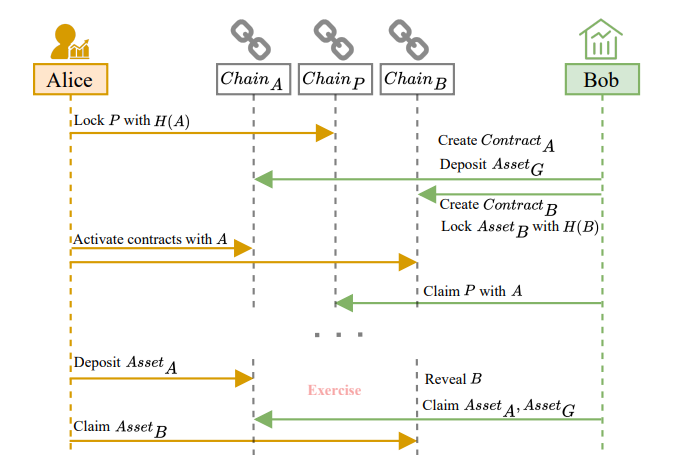
Suppose Alice and Bob reach an agreement that Alice pays Bob 𝑃 as a premium on a chain denoted by 𝐶ℎ𝑎𝑖𝑛𝑃 . The option takes effective at 𝑇𝐴 meaning that Alice obtains the right to exchange 𝐴𝑠𝑠𝑒𝑡𝐴 for 𝐴𝑠𝑠𝑒𝑡𝐵 before 𝑇𝐸. Bob’s guarantee is 𝐴𝑠𝑠𝑒𝑡𝐺 .
The protocol involves two kinds of asset settlement: first for option establishment (or activation, we use them interchangably) and second for option exercise. We therefore introduce two secrets:
(1) Activation secret 𝐴, used for Alice to pay the premium and activate the option; and (2) Exercise secret 𝐵, used for Alice to pay 𝐴𝑠𝑠𝑒𝑡𝐴 to Bob in exchange for 𝐴𝑠𝑠𝑒𝑡𝐵 when the option is exercised. Secret 𝐴 is generated by Alice and 𝐵 is generated by Bob.
The protocol is divided into two phases. Figure 2 shows the execution process of this protocol if both parties are honest.
(1) Setup phase: Alice and Bob activate an option. Alice obtains option and Bob obtains premium.
(2) Exercise/Abandon phase: Alice can either exercise the option or abandon it.
In the setup phase, Alice and Bob will establish this option similarly to a vanilla HTLC. Alice locks 𝑃 with a hashlock 𝐻(𝐴) in a contract on any chain. Bob creates two contracts, 𝐶𝑜𝑛𝑡𝑟𝑎𝑐𝑡𝐴 on 𝐶ℎ𝑎𝑖𝑛𝐴 and 𝐶𝑜𝑛𝑡𝑟𝑎𝑐𝑡𝐵 on 𝐶ℎ𝑎𝑖𝑛𝐵, which are used in the option. The option remains inactive until Alice reveals the activation secret 𝐴 before 𝑇𝐴, at which point the state updates to active and Bob gets Alice’s premium. 𝐶𝑜𝑛𝑡𝑟𝑎𝑐𝑡𝐴 holds Bob’s guarantee, 𝐴𝑠𝑠𝑒𝑡𝐺 , until the option expires. If Alice exercises the option and Bob fulfills his obligation by revealing the exercise secret 𝐵, 𝐴𝑠𝑠𝑒𝑡𝐺 is refunded to Bob. If Bob fails to fulfills his obligation, 𝐴𝑠𝑠𝑒𝑡𝐺 will be transferred to Alice. 𝐶𝑜𝑛𝑡𝑟𝑎𝑐𝑡𝐵 locks Bob’s collateral, 𝐴𝑠𝑠𝑒𝑡𝐵, using 𝐻(𝐵).
I. Setup Phase.
(1) Alice randomly selects a secret 𝐴 as activation secret, and computes its hash value 𝐻(𝐴). Bob generates 𝐵 and 𝐻(𝐵), which serve as the exercise secret and hashlock.
(2) Alice locks 𝑃 with hashlock 𝐻(𝐴) on the agree-upon𝐶ℎ𝑎𝑖𝑛𝑃 with timeout 𝑇𝐴 + Δ.
(3) If Bob observes that Alice has honestly deposited the premium, Bob should, at any time before 𝑇𝐴 − Δ:
(a) Create 𝐶𝑜𝑛𝑡𝑟𝑎𝑐𝑡𝐴 on 𝐶ℎ𝑎𝑖𝑛𝐴 and 𝐶𝑜𝑛𝑡𝑟𝑎𝑐𝑡𝐵 on 𝐶ℎ𝑎𝑖𝑛𝐵. These contracts are initially in an inactive state, and record the holder and writer, activation time 𝑇𝐴 and option expiration time 𝑇𝐸.
(b) Escrow the guarantee 𝐴𝑠𝑠𝑒𝑡𝐺 on 𝐶ℎ𝑎𝑖𝑛𝐴, and lock principal 𝐴𝑠𝑠𝑒𝑡𝐵 on 𝐶ℎ𝑎𝑖𝑛𝐵 with hashlock 𝐻(𝐵).
(4) If Alice observes that Bob has created contracts and made deposits, Alice reveals 𝐴 at 𝑇𝐴 on both chains to activate the option. If not, transaction aborts, Bob calls refund() and retrieves 𝐴𝑠𝑠𝑒𝑡𝐺 and 𝐴𝑠𝑠𝑒𝑡𝐵. Alice refunds 𝑃.
II. Exercise/Abandon Phase.
(1) Exercise: If Alice wants to exercise the option at 𝑇𝐵 before expiration, she calls exercise() and deposits 𝐴𝑠𝑠𝑒𝑡𝐴 into 𝐶𝑜𝑛𝑡𝑟𝑎𝑐𝑡𝐴, then within one Δ:
(a) If Bob reveals 𝐵 and calls fulfill() on 𝐶𝑜𝑛𝑡𝑟𝑎𝑐𝑡𝐴, then he obtains both 𝐴𝑠𝑠𝑒𝑡𝐴 and 𝐴𝑠𝑠𝑒𝑡𝐺 . Upon observing 𝐵, Alice obtains 𝐴𝑠𝑠𝑒𝑡𝐵 with 𝐵 from 𝐶𝑜𝑛𝑡𝑟𝑎𝑐𝑡𝐵.
(b) If Bob does not reveal 𝐵, Alice calls claim() on𝐶𝑜𝑛𝑡𝑟𝑎𝑐𝑡𝐴 after 𝑇𝐵 + Δ to receive 𝐴𝑠𝑠𝑒𝑡𝐺 as compensation.
(2) Abandon: If Alice does not call exercise() before or at 𝑇𝐸, then the option is abandoned and Bob can call refund() on 𝐶𝑜𝑛𝑡𝑟𝑎𝑐𝑡𝐴 and 𝐶𝑜𝑛𝑡𝑟𝑎𝑐𝑡𝐵 to refund 𝐴𝑠𝑠𝑒𝑡𝐺 and 𝐴𝑠𝑠𝑒𝑡𝐵.
Timeouts. The latest deadline 𝑇𝐵 is no later than 𝑇𝐸. If Bob fails to fulfill his obligations, then Alice receives 𝐴𝑠𝑠𝑒𝑡𝐺 by 𝑇𝐸 + 2Δ. Therefore, the lock period for 𝐴𝑠𝑠𝑒𝑡𝐺 in 𝐶𝑜𝑛𝑡𝑟𝑎𝑐𝑡𝐴 is 𝑇𝐸 +Δ if Alice waives the option, or extends to𝑇𝐸 +2Δ if Alice exercises the option. Alice exercises the option and receives 𝐴𝑠𝑠𝑒𝑡𝐵 by𝑇𝐸 +2Δ. Therefore, the lock period for 𝐴𝑠𝑠𝑒𝑡𝐵 in 𝐶𝑜𝑛𝑡𝑟𝑎𝑐𝑡𝐵 is 𝑇𝐸 + 2Δ.
4.2.1 Integration: Efficient Cross-Chain Options without Upfront Holder Collateral. We incorporate the efficient option transfer protocol to enable a collateral-free option transfer process. From the option transfer perspective, the roles of the holder and writer are reversed, as Bob owns the exercise secret. Bob deposits 𝐴𝑠𝑠𝑒𝑡𝐺 and 𝐴𝑠𝑠𝑒𝑡𝐵 in 𝐶𝑜𝑛𝑡𝑟𝑎𝑐𝑡𝐴 and 𝐶𝑜𝑛𝑡𝑟𝑎𝑐𝑡𝐵. In the transfer of Bob’s position, hashlock 𝐻(𝐵) must remain consistent.
Take Bob transferring writer to Dave as an example. It is similar to the Protocol 4.1.1 with three notable differences. Suppose Bob reaches an agreement with Dave to transfer the writer position. Dave is able to buy Bob’s risky asset with its obligation at the price of 𝑊 𝑟𝑖𝑡𝑒𝑟𝐹𝑒𝑒 before or at 𝑇𝑊 . First, Dave must choose a new hashlock as the exercise secret, and similarly, Bob needs to use his private key 𝑠𝑘𝐵 to sign Dave’s new hashlock 𝐻(𝐷), which means message 𝑚 = (𝑎, (Dave.𝑎𝑑𝑑𝑟𝑒𝑠𝑠, 𝐻(𝐷), 𝑝𝑘𝐷 )). Second, Alice can use Bob’s private key 𝑠𝑘𝐵 to reclaim 𝐴𝑠𝑠𝑒𝑡𝐵 and guarantee, 𝐴𝑠𝑠𝑒𝑡𝐺 . Third, if Alice wants to exercise the option and makes the deposit after Bob reveals the signature during the transfer process, the transfer continues, and Dave must forward the signature to obtain the writer’s position. Dave should fulfill his obligation and reveal the exercise secret at 𝑇𝑊 − Δ on 𝐶𝑜𝑛𝑡𝑟𝑎𝑐𝑡𝐴.

As a result of the support for concurrent bidding, our protocol can effectively defend against phantom bid attack. In phantom bid attack, an adversary creates multiple virtual buyers who offer higher prices but do not finalize the transfer. In the previous protocol [12] which attempts to transfer the option to a buyer sequentially, in face of such an attack, the option holder/writer cannot sell their positions in a reasonable time since the virtual buyers are exhausting the option transfer window.
With our proposed protocol, an adversary option buyer cannot launch this attack. This is due to the use of a signature for option transfer settlement, rather than a hashlock used in the previous protocol. By this signature scheme, once a buyer is chosen by the seller, the option transfer can be finalized. There is no time window for the buyer to choose to finalize the option transfer or abort.
Authors:
(1) Zifan Peng, The Hong Kong University of Science and Technology (Guangzhou) Guangzhou, Guangdong, China ([email protected]);
(2) Yingjie Xue, The Hong Kong University of Science and Technology (Guangzhou) Guangzhou, Guangdong, China ([email protected]);
(3) Jingyu Liu, The Hong Kong University of Science and Technology (Guangzhou) Guangzhou, Guangdong, China ([email protected]).
This paper is available on arxiv under CC BY 4.0 license.

