Table of Links
-
Protocol
-
Security Analysis
A. Codes
B. Proofs
4 PROTOCOL
Due to the complexity of efficient holder collateral-free options, we elaborate on the protocol gradually. We first introduce the efficient transfer of an option in Section 4.1. Next, we outline how to achieve holder collateral-free cross-chain options in Section 4.2. Finally, we show the efficient, holder collateral-free option protocol.
4.1 Efficient Option Transfer Protocol
Option Initialization. Firstly, we illustrate an efficient option transfer protocol in an HTLC-based option. Assume Alice and Bob initialize an HTLC-based option as the holder and writer respectively. In this option, Alice locks 𝐴𝑠𝑠𝑒𝑡𝐴 on 𝐶ℎ𝑎𝑖𝑛𝐴, intending to transfer it to Bob if a preimage of 𝐻(𝐴) is presented before 𝑇𝐸 + Δ. Bob locks 𝐴𝑠𝑠𝑒𝑡𝐵 on 𝐶ℎ𝑎𝑖𝑛𝐵, intending to transfer it to Alice if a preimage of 𝐻(𝐴) is presented before𝑇𝐸, where𝑇𝐸 is the expiration time of this option. Alice owns the preimage 𝐴. In addition, Alice performs 𝐾𝑒𝑦𝐺𝑒𝑛(1 𝜆 ) → (𝑝𝑘𝐴, 𝑠𝑘𝐴), which acts as a transfer key pair3 , which are used for DAPS and misbehavior detection. 𝑝𝑘𝐴 is recorded in both contracts. The transfer key is used by Alice when transferring ownership to another party. A signature generated by 𝑠𝑘𝐴 can be used to replace the contract holder, the hashlock, and the new transfer public key. Similarly, Bob creates a transfer key and records it on chains. Alice and Bob agree in advance on a value (e.g., a 256-bit random number) to serve as the message address 𝑎 recorded in the contracts for the DAPS. We take holder position transfer as an example to illustrate this transfer protocol.
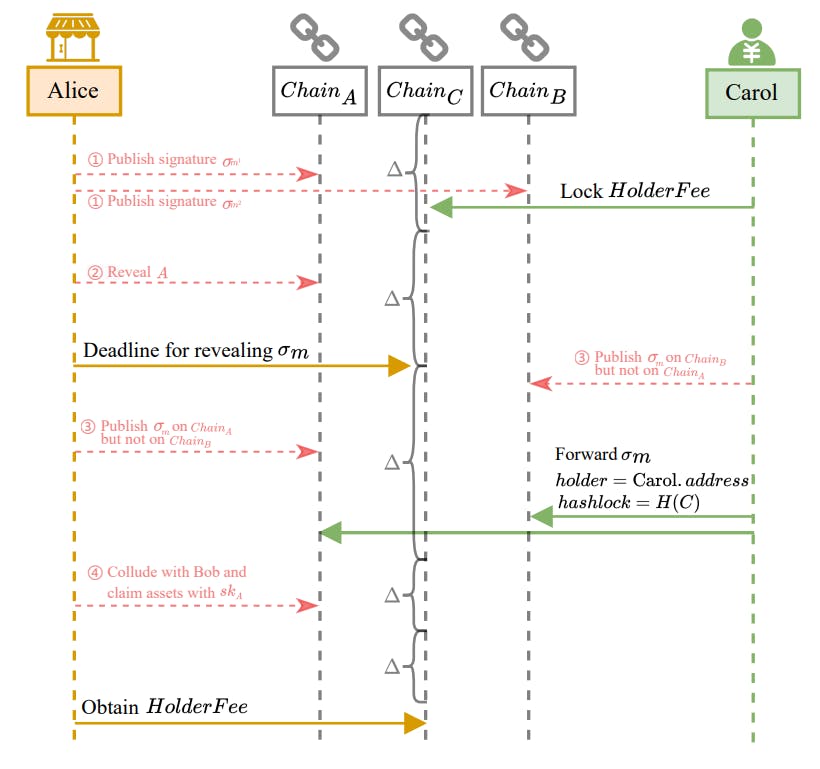
4.1.1 Transfer Holder’s Position. Suppose Alice reaches an agreement with Carol to transfer the holder position on or before time 𝑇𝐻 , with a charge of 𝐻𝑜𝑙𝑑𝑒𝑟𝐹𝑒𝑒 on 𝐶ℎ𝑎𝑖𝑛𝐶. Carol performs 𝐾𝑒𝑦𝐺𝑒𝑛(1 𝜆 ) → (𝑝𝑘𝐶, 𝑠𝑘𝐶) to generate a new transfer key pair. Carol deposits 𝐻𝑜𝑙𝑑𝑒𝑟𝐹𝑒𝑒 in 𝐶𝑜𝑛𝑡𝑟𝑎𝑐𝑡𝐶. This contract requires a signature of 𝑚 = (𝑎, 𝑝), where message payload 𝑝 = (Carol.𝑎𝑑𝑑𝑟𝑒𝑠𝑠, 𝐻(𝐶), 𝑝𝑘𝐶), signed by 𝑠𝑘𝐴 to unlock and transfer the 𝐻𝑜𝑙𝑑𝑒𝑟𝐹𝑒𝑒 to Alice. Besides, 𝐶𝑜𝑛𝑡𝑟𝑎𝑐𝑡𝐶 records 𝐻(𝐴), specifying that 𝐻𝑜𝑙𝑑𝑒𝑟𝐹𝑒𝑒 is refunded to Carol if Carol can reveal 𝐴 (meaning that Alice has exercised the option). Instead withdraw immediately, after Alice reveals a signature to redeem 𝐻𝑜𝑙𝑑𝑒𝑟𝐹𝑒𝑒 , she must wait for 3Δ to elapse. We refer to this period as the Withdrawal Delay Period. The protocol consists of two phases, Figure 1 illustrates the position transferring process:
(1) Reveal Phase: Carol locks the transfer fee and Alice attempts to withdraw the transfer fee with her signature.
(2) Consistency Phase: Carol forwards the signature to replace the holder and Alice withdraws the transfer fee after the withdrawal delay period.
I. Reveal Phase.
(1) Alice generates signature by 𝑆𝑖𝑔𝑛(𝑠𝑘𝐴,𝑚) → 𝜎𝑚, where 𝑚 equals to (𝑎, (Carol.𝑎𝑑𝑑𝑟𝑒𝑠𝑠, 𝐻(𝐶), 𝑝𝑘𝐶)).
(2) If Alice wants to transfer her option to Carol, Alice sends 𝜎𝑚 in Contract𝐶 by invoking the function reveal() and wait for 3Δ (withdrawal delay period). If she does not like to complete the trade between Carol, she does not reveal 𝜎𝑚. The 𝐻𝑜𝑙𝑑𝑒𝑟𝐹𝑒𝑒 will be refunded to Carol after 𝑇𝐻 .
II. Consistency Phase.
(1) Carol4 forwards 𝜎𝑚 to both 𝐶𝑜𝑛𝑡𝑟𝑎𝑐𝑡𝐴 and 𝐶𝑜𝑛𝑡𝑟𝑎𝑐𝑡𝐵 directly, attempting to call the function transferHolder() to replace the holder to Carol, the hashlock to 𝐻(𝐶), and holder’s transfer public key to 𝑝𝑘𝐶.
(2) Alice calls withdraw() to obtain the 𝐻𝑜𝑙𝑑𝑒𝑟𝐹𝑒𝑒 in 𝐶𝑜𝑛𝑡𝑟𝑎𝑐𝑡𝐶 after the withdrawal delay period.
If all parties perform honestly, Alice is able to receive 𝐻𝑜𝑙𝑑𝑒𝑟𝐹𝑒𝑒 and holder is changed to Carol. However, there are possible contingent events or dishonest scenarios:
• If Alice exercises the option during the transfer process and reveals the preimage 𝐴 before 𝑇𝐻 , Carol can refund the 𝐻𝑜𝑙𝑑𝑒𝑟𝐹𝑒𝑒 from 𝐶𝑜𝑛𝑡𝑟𝑎𝑐𝑡𝐶 using 𝐴 during the withdrawal delay period.
• If different signatures with the same message address 𝜎𝑚′ ≠ 𝜎𝑚, are submitted on 𝐶ℎ𝑎𝑖𝑛𝐴 and 𝐶ℎ𝑎𝑖𝑛𝐵 (e.g., if Alice submits two different signatures or sells the option to multiple parties), any one can call 𝐸𝑥𝑡𝑟𝑎𝑐𝑡(𝑝𝑘,𝑚′ , 𝜎𝑚′,𝑚, 𝜎𝑚) → 𝑠𝑘𝐴 to get 𝑠𝑘𝐴. 𝑠𝑘𝐴 is the secret transfer key of Alice. Whoever gets 𝑠𝑘𝐴 means that Alice misbehaves. We can use this as an evidence for fair settlement of funds.
– Carol can call reclaim() and obtain the 𝐻𝑜𝑙𝑑𝑒𝑟𝐹𝑒𝑒 with 𝑠𝑘𝐴 during the withdrawal delay period.
– Bob can use 𝑠𝑘𝐴 to claim both 𝐴𝑠𝑠𝑒𝑡𝐴 and 𝐴𝑠𝑠𝑒𝑡𝐵. If a signature has not been submitted, Bob can claim it anytime. If a signature has been submitted, Bob needs to send 𝑠𝑘𝐴 within one Δ after the signature submission.
• If Carol reveals 𝜎𝑚 on only 𝐶𝑜𝑛𝑡𝑟𝑎𝑐𝑡𝐴 or 𝐶𝑜𝑛𝑡𝑟𝑎𝑐𝑡𝐵, Bob can forward the signature to the other contract.
Timeouts. The transfer contract must be created no later than 𝑇𝐻 − 3Δ, and the reveal phase should be completed by 𝑇𝐻 − 2Δ to ensure that the option can be transferred to Carol at 𝑇𝐻 . In the consistency phase, if any misbehavior occurs, it should be reported to the contract by 𝑇𝐻 + Δ. If Bob does not claim assets on 𝐶ℎ𝑎𝑖𝑛𝐴 and 𝐶ℎ𝑎𝑖𝑛𝐵 with 𝑠𝑘𝐴, then it implies transfer complete. Overall, a total transfer time of 4Δ is required. In other words, the transfer protocol must initiate no later than 𝑇𝐸 − 4Δ. The unlocking condition for 𝐶𝑜𝑛𝑡𝑟𝑎𝑐𝑡𝐶 is summarized in Table 2.

4.1.2 How misbehaviors are handled securely in the protocol. Here we show how this protocol handles misbehaviour and protect each party’s interests by ensuring a fair payoff for honest parties. A more rigorous analysis is shown in Appendix B.1. First, we consider each party acting maliciously on their own.
• If Alice provides two different signatures to different buyers, as shown in 1, Bob can extract 𝑠𝑘𝐴 and submit it to obtain 𝐴𝑠𝑠𝑒𝑡𝐴 and 𝐴𝑠𝑠𝑒𝑡𝐵, and Carol can reclaim the transfer fee with 𝑠𝑘𝐴. In that case, Bob does not lose his 𝐴𝑠𝑠𝑒𝑡𝐵 and Carol does not lose her transfer fee.
• If Alice reveals𝐴 at the same time during the transfer process, as shown in 2, Carol can use 𝐴 to reclaim 𝐻𝑜𝑙𝑑𝑒𝑟𝐹𝑒𝑒. She does not lose anything. The option is exercised, and swap happens between Alice and Bob.
• If Alice or Carol publishes one signature exclusively on either 𝐶𝑜𝑛𝑡𝑟𝑎𝑐𝑡𝐴 or 𝐶𝑜𝑛𝑡𝑟𝑎𝑐𝑡𝐵, as shown in 3, Bob can forward this signature to another chain to make sure the hashlocks and option holders are consistent on two chains.
Next, we consider scenarios where collusion exists.
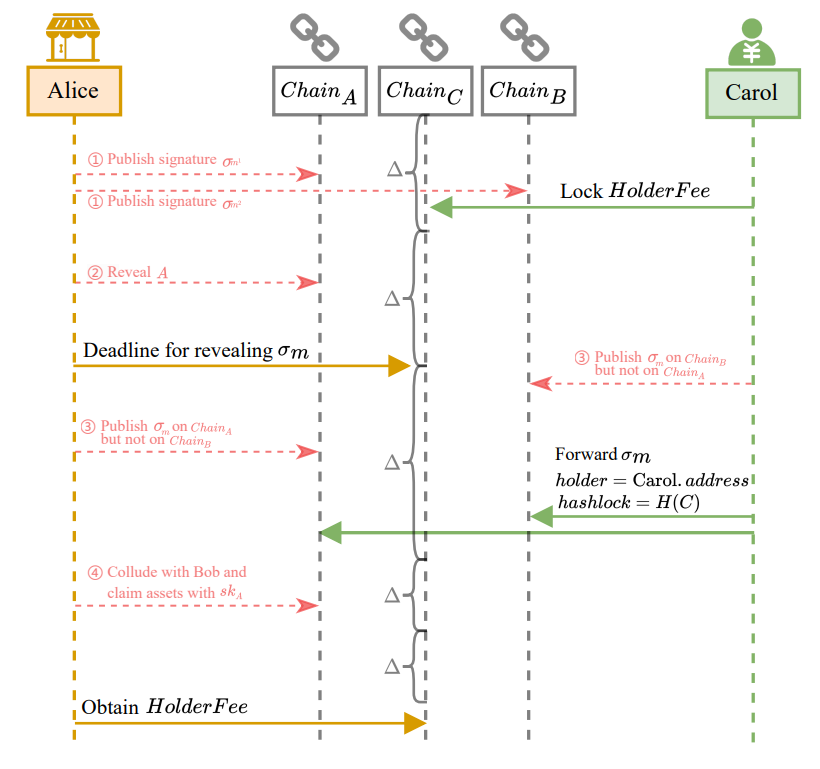
• If Alice and Bob collude, they can use 𝑠𝑘𝐴 or 𝐴 to withdraw 𝐴𝑠𝑠𝑒𝑡𝐴 and 𝐴𝑠𝑠𝑒𝑡𝐵 as shown in 4. Carol can observe 𝑠𝑘𝐴 or 𝐴 and withdraw 𝐻𝑜𝑙𝑑𝑒𝑟𝐹𝑒𝑒 during the withdrawal delay period.
• If Alice and Carol collude, they use two signatures to change the hashlock. During the withdrawal delay period, Bob can obtain 𝐴𝑠𝑠𝑒𝑡𝐴 and 𝐴𝑠𝑠𝑒𝑡𝐵 using the extracted 𝑠𝑘𝐴, which is reduced to 1.
• If Bob and Carol collude, they cannot do anything harm. Since Alice will only reveal one valid signature, Alice will receive 𝐻𝑜𝑙𝑑𝑒𝑟𝐹𝑒𝑒 from Carol.
4.1.3 Transfer Writer’s Position. Transferring the writer’s position is similar but simpler because Bob does not possess the preimage of the hashlock. Bob, with the transfer key pair (𝑝𝑘𝐵, 𝑠𝑘𝐵), can sign the message 𝑚 = (𝑎, (Dave.𝑎𝑑𝑑𝑟𝑒𝑠𝑠, 𝑝𝑘𝐷 )) using 𝑠𝑘𝐵 to collect the transfer fee, where 𝑝𝑘𝐷 is a new transfer key for Dave. Transferring writer’s position does not update the hashlock used in the option exercise. Thus, Alice’s option is not influenced except the change of new option writer.
Authors:
(1) Zifan Peng, The Hong Kong University of Science and Technology (Guangzhou) Guangzhou, Guangdong, China ([email protected]);
(2) Yingjie Xue, The Hong Kong University of Science and Technology (Guangzhou) Guangzhou, Guangdong, China ([email protected]);
(3) Jingyu Liu, The Hong Kong University of Science and Technology (Guangzhou) Guangzhou, Guangdong, China ([email protected]).
This paper is available on arxiv under CC BY 4.0 license.
[3] Logically, the transfer key is not used for receiving coins as "identities" in blockchains.
[4] Any party can forward this signature, as Alice may transfer ownership to any party.