This paper is available on arxiv under CC BY 4.0 DEED license.
Authors:
(1) Ehsan Toreini, University of Surrey, UK;
(2) Maryam Mehrnezhad, Royal Holloway University of London;
(3) Aad Van Moorsel, Birmingham University.
Table of Links
Implementation and Performance Analysis
3 FaaS Architecture
In this Section, we present the architecture of our system (Fig. 1) and describe its features. The FaaS architecture includes stakeholders in three roles: A) ML System: a system that owns the data and the ML algorithm, B) Fairness Auditor Service: a service that computes the fair performance of the ML system, and C) Universal Verifier: anyone who has the technical expertise and motivation to verify the auditing process.
3.1 Threat Model
The design and implementation of the security of parties implementing the respective protocol roles (ML system, Fairness Auditor Service, and Universal Verifier) (Fig. 1) are independent of each other. The inter–communications that happen between the roles assumes no trust between parties; thus, all their claims must be accompanied with validation proofs (for which we will use ZKP). We assume the Auditor System is vulnerable to different attacks and not trustworthy. Thus, the data stored on the Fairness Auditor System must be encrypted, tamper-proof and verifiable at all stages. Moreover, we assume the communication channel between the ML system and fairness auditor is not protected. Therefore, the sensitive data must be encrypted before the transmission starts. However, there will be an agreement on the cryptographic primitives at the pre–setting stage in the protocol sequence.
In FaaS, we assume that the ML system is honest in sending the cryptograms of the original labels of the dataset samples. One might argue against such assumption and discuss that the ML system might intend to deceive the Auditor Service, and by extension the verifiers, by modifying the actual labels of the dataset. For instance, the ML system would provide the cryptograms of the actual labels and the predicted ones as similar to each other as possible so that the auditor concludes the algorithms are fair. This is an interesting area for further research. For instance, it may be addressed by providing the cryptograms of the actual labels to the Auditor Service independently e.g. the verifier may own a dataset it provides to a ML system. The verifier then separately decides the desired values for the actual labels and feeds these to the Auditor service. In this way, it is far less clear to the ML system how to manipulate the data it sends to the auditor, since some of the labels come from elsewhere.
The internal security of the roles is beyond FaaS. The ML system itself needs to consider extra measures to protect its data and algorithms. We assume the ML system does present the data and predictions honestly. This is a reasonable assumption since the incentives to perform ethically is in contrast to being dishonest when participating in fairness auditing process. This is discussed more in the Discussion Section.
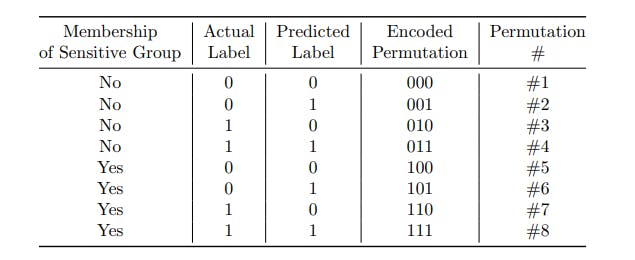
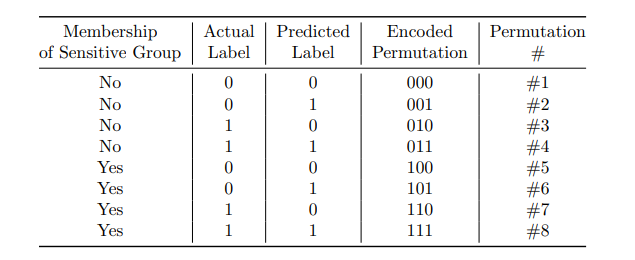
Table 2: Possible permutations of 3-bit representation of an entry in the original data.
3.2 Protocol Overview
The main security protocol sequence is between the ML system and Fairness Auditing Service or auditor in short form. Note that although we suggest three roles in our architecture, the communications are mainly between the above two roles, and any universal verifier can turn to the auditor service (which represents the fairness board), if they want to challenge the computations.
The ML system is responsible for the implementation and execution of the ML algorithm. It has data as input and performs some prediction (depending on the use case and purpose) that forms the output (Fig. 1). The Fairness Auditor Service receives information from the ML system, evaluates its fairness performance by computing a fairness metric. Then, it returns the result for the metric back to the ML system. It also publishes the calculations in a fairness board for public verification. The public fairness board is a publicly accessible, read-only fairness board (e.g. a website). The auditor only has the right to append data (and the sufficient proofs) to the fairness board. Also, the auditor verifies the authenticity, correctness and integrity of data before publishing it.
3.3 Protocol Sequence
This protocol has three stages: setup, cryptogram generation and fairness metric computation.
3.3.1 Phase I: Setup
In this phase, the ML System and Auditor agree on the initial settings. We assume the protocol functions in multiplicative cyclic group setting (i.e. Digital Signature Algorithm (DSA)–like group [18]), but it can also function in additive cyclic groups (i.e. Elliptic Curve Digital Signature Algorithm (ECDSA)–like groups [18]). The auditor and ML system publicly agree on (p, q, g) before the start of the protocol. Let p and q be two large primes where q|(p − 1). In a multiplicative cyclic group (Z ∗ p ), Gq is a subgroup of prime order q and g is its generator. For simplicity, we assume the Decision Diffie–Hellman (DDH) problem is out of scope [31].
Next, the ML system generates a public/private pair key by using DSA or ECDSA and publishes the public keys in the fairness board. The protection the private key pair depends on the security architecture of the ML system and we assume the private key is securely stored in an industrial standard practice (e.g. using the secure memory module on board).
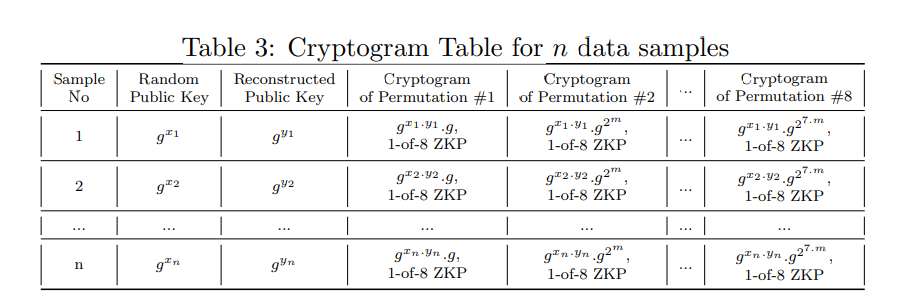
Cryptogram Table: After initial agreements, the ML system produces a cryptogram table with n rows corresponding to the number of samples in their test dataset. We will refer to this table as cryptogram table in the rest of this paper. In case the ML system does not want to reveal the number of the samples in the test set, the auditor and the ML system can publicly agree on n. In this case, n must be big enough so that the universal verifiers are satisfied with the outcome.
Each row in the cryptogram table summarises three parameters: (1) protected group membership status, (2) its actual label and (3) predicted label by the ML model. Each row contains the encrypted format of the three parameters along with proofs of its correctness. A cryptogram table in the setup phase is shown in Table 3. In the simplest case, each parameter is binary. Therefore, the combined parameters will generate eight permutations in total. In the setup phase, the table is generated to contain all eight possible permutations and their proofs for each data sample. The total structure of the permutations are shown in Table 2. Each row will satisfy four properties: (a) one can easily verify if a single cryptogram is the encrypted version of one of the eight possible permutations, (b) while verifiable, if only one single cryptogram selected, one cannot exert which permutations the current cryptogram represents, (c) for each two cryptograms selected from a single row, anyone will be able to distinguish each from one another, and (d) given a set of cryptograms arbitrarily select from each row as a set, one can easily check how many cases for each “permutation” are in the set.
The generation of the cryptogram table functions are based on the following sequence:
Step (1): For each of the n samples, the system generates a random public key g xi where xi is the private key and xi ∈ [1, q − 1].

Step (3): The corresponding column number that equals the decimal value of the binary encoding is selected from the cryptogram table to complete the fairness auditing table( as shown in Table 2).
Finally, the generated fairness auditing table is digitally signed by the ML system and then is sent over the Fairness auditing service.
3.3.3 Phase III: Fairness Evaluation
First, the fairness auditing service receives the fairness auditing table, verifies the digital signature and the ZKPs, and publishes the contents in the fairness board.

At this point, we expand each of these equation components to compare them together.

This process is computationally heavy especially when the number of data samples in the fairness auditing table is large. In this case, the fairness auditor can delegate the declaration of the permutation number to the ML system. The auditor still receives the fairness auditing table and the relevant ZKPs. It can store the fairness auditing table to the fairness board, compute the fairness, and verify the correctness of the declared permutation numbers. The universal verifier can follow the same steps to verify the fairness metric computations through the fairness auditing table that is publicly accessible via fairness board.
At the end of this stage, the auditor uses the acquired numbers to compute the fairness metric and release the information publicly. The number of each permutation denotes the overall performance of the ML algorithm for each of the groups with protected attribute. Table 4 demonstrates the permutations and how it relates to the fairness metric of the ML system. The cryptogram table and the results will be published on the fairness board (Fig. 1)