This paper is available on arxiv under CC BY-SA 4.0 DEED license.
Authors:
(1) Lana L. Blaschke, Earth System Modelling, School of Engineering and Design, Technical University of Munich, Munich, Germany, Potsdam Institute for Climate Impact Research, Potsdam, Germany and [email protected];
(2) Da Nian, Potsdam Institute for Climate Impact Research, Potsdam, Germany;
(3) Sebastian Bathiany, Earth System Modelling, School of Engineering and Design, Technical University of Munich, Munich, Germany, and Potsdam Institute for Climate Impact Research, Potsdam, Germany;
(4) Maya Ben-Yami, Earth System Modelling, School of Engineering and Design, Technical University of Munich, Munich, Germany, and Potsdam Institute for Climate Impact Research, Potsdam, Germany;
(5) Taylor Smith, Institute of Geosciences, University of Potsdam, 14476 Potsdam, Germany;
(6) Chris A. Boulton, Global Systems Institute, University of Exeter, EX4 4QE Exeter, UK ;
(7) Niklas Boers, Earth System Modelling, School of Engineering and Design, Technical University of Munich, Munich, Germany, Potsdam Institute for Climate Impact Research, Potsdam, Germany, Global Systems Institute, University of Exeter, EX4 4QE Exeter, UK, and Department of Mathematics, University of Exeter, EX4 4QF Exeter, UK.
Table of Links
- Abstract and Introduction
- Materials and Methods
- Data
- Results
- Conclusions, Open Research Section and Conflict of Interest/Competing Interests
- Author Contributions, Supplementary Information, Acknowledgments and References
- Additional Insight from the Conceptual Model
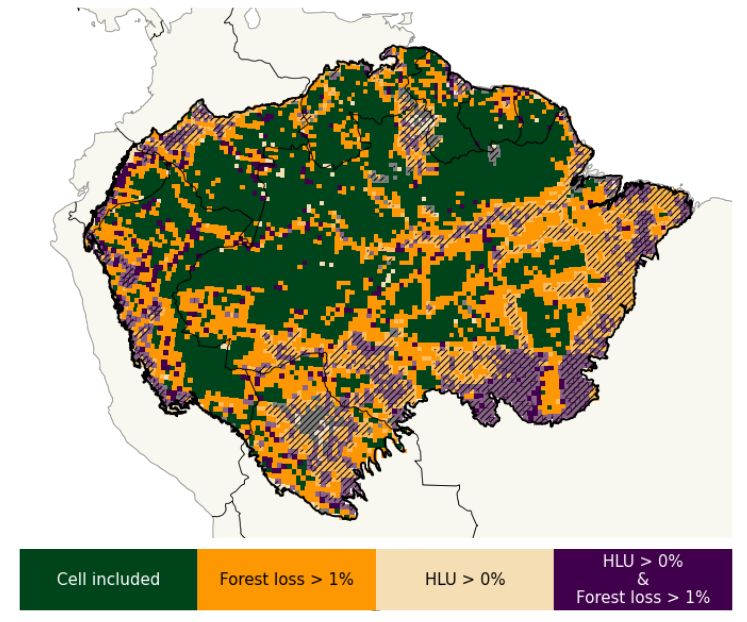
- AMSR2 until 2022 Excluded Due to Missing Human Land Use Data
- Investigation of Resilience Loss in AMSR2’s X-Band
- Results Proving Robustness
- Potential Driving Forces and Sources of Bias
MATERIALS AND METHODS
Description and parametrization of the conceptual model
To demonstrate the relevance of the three indicators of CSD in a setting like the ARF, we slightly modify a previously introduced conceptual model of atmosphere-vegetation interaction (Bathiany et al., 2013b). The vegetation dynamics of the model are inspired by the global dynamical vegetation model VECODE (Brovkin et al., 1997, 2002, 1998; Bathiany et al., 2013a), which is based on an empirical relationship of vegetation cover fraction and atmospheric conditions.
In particular, the equilibrium vegetation V∗ is a monotonic (sigmoidal) function of precipitation, see Equation 1. The vegetation dynamics are simulated as a linear relaxation toward this empirical equilibrium and the equilibrium vegetation V∗ is a direct function of total incoming precipitation Pi in [mm/year], namely
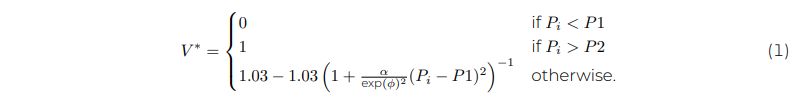
Here, Pi represents the amount of precipitation in a cell i, as the spatial extension of our model consists of 10 cells. While VECODE is based on an empirical relationship of vegetation cover fraction based on atmospheric conditions, we here interpret the vegetation variable V∗ as a property linked to the tree cover in the Amazon (e.g., tree cover fraction or biomass). We motivate this interpretation by the conceptual nature of the model approach, and the fact that tree coverage in the original VECODE version is modeled by a very similar approach as vegetation coverage (with a curve that is shifted to higher precipitation rates). Making the model more complex by distinguishing plant types would hence not add to our analysis.
The parameters P1 and P2 in Eq. 1 are given by
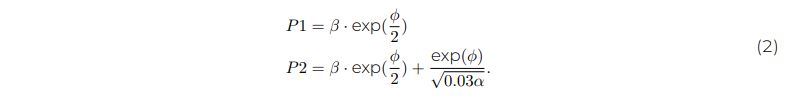
Parametrization is chosen in a similar way to Bathiany et al. (2013b) but adapted such that the range of bistability in dependence of precipitation is closer to that in the ARF. Namely, the parameters are α = 0.0011, β = 280, and ϕ = 2.45. Thus, the vegetation Vi ∈ [0, 1] of a cell i at time t + 1 is given by
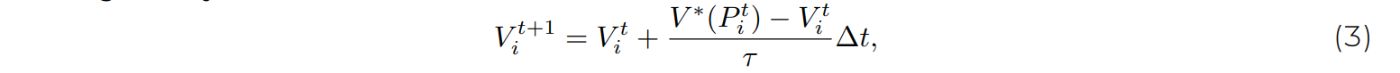

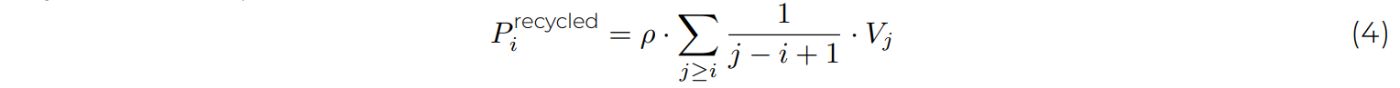

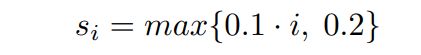

where the standard deviation of the white noise is set to σ = 20. A visualization of thedeterministic part of precipitation in the model is given in Fig. 2.
To mimic a climate change scenario with declining moisture inflow from the Atlantic ocean, the bifurcation parameter B decreases linearly from 1100 to 990 over time in our model runs. One should note that due to the different magnitudes of moisture inflow from moisture recycling, the critical value of the control parameter B differs between the cells. The interaction of vegetation and precipitation leads to the stability diagram shown in Fig. S1 and to a transition to a low vegetation state once the critical threshold of precipitation is crossed.
While the characteristic relaxation time in VECODE is climate dependent, we here follow Bathiany et al. (2013b) and set it to a constant value (here: τ = 100 years), which allows a more straightforward interpretation of CSD in the model. The constant τ resembles the inherent timescale of the vegetation system. The time step ∆t = 1 corresponds to one year in accordance with P representing mean annual precipitation. While this contradicts the VOD observations that are available for 10 years, with fluctuations happening on monthly scale, it must be pointed out here that the time scale difference does not matter as a time step unit could be interpreted as e.g. days as well.
Realizations of the model are the numerical approximations of the solutions of the given equations by an Euler-Maruyama-scheme with random white noise added to the precipitation. As this analysis focuses on measures that are valid in the vicinity of the fixed point, equilibrium runs are performed. For each change in the bifurcation parameter, 1000 steps of the EulerMaruyama scheme are executed, of which the last one is added to the data set as one time step. Moreover, the data of the first time step are the result of 10000 steps with initial values randomly distributed around the fixed point. The simulations shown are based on 1000 time steps. All results are based on 1000 realizations of the stochastic model.
Resilience analysis
To assess changes in resilience based on the concept of CSD, we de-trend and de-season the data sets and calculate the variance, AC1 and spatial correlation in sliding windows. The change is then defined as the time series’ linear trends.
De-trending and de-seasoning
All indicators of CSD are based on perturbations of the state variable around its equilibrium. Hence, the variable to analyze must not contain any trend or seasonality. For the conceptual model, this is achieved by subtracting the equilibrium vegetation state of the corresponding cell from its vegetation state in each realization. For the satellite vegetation data, the trend and seasonality of each VI in each grid cell are removed by applying the Seasonal-Trend decomposition using LOESS (STL). The parameters are set to the default values proposed in Cleveland et al. (1990), but an additional analysis confirms that the general results are robust against variation in the parametrization.
Detection of resilience changes
The actual indicators of resilience are then computed on sliding windows. For each window, variance and AC1 are calculated grid-cell-wise, with correlation referring to the Pearson correlation coefficient throughout this study. The spatial correlation of a cell i is defined as

For the conceptual model, the size of the windows is set to 100 time steps. In the real data, defining the sliding window size must be done with consideration of the total length of the time series. Large window sizes ensure robust indicator values, but leave less time steps to calculate their corresponding trends or tendencies. In the main analysis, the window size is 5 years, equivalent to 60 data points. The trade-off is especially high in the case of the single-sensor data considered here due to their short availability. Yet, the results are robust with regards to the window size.
To evaluate the change in resilience over time, the development of the corresponding indicators of CSD over time is of interest. This change over time is then quantified by the trend, which is defined as the slope of a linear regression. While the trend might be biased by large jumps in comparison to many small changes, the Kendall τ correlation coefficient assesses the time series’ tendency, measured as the steadiness of the increase. All results are stated in terms of trends, but are robust when compared to results assessed by the tendency.
Time of emergence
To assess the reliability of the indicators, we define the time of emergence (ToE) as the time a significant trend emerges for the first time. To calculate the ToE for the conceptual model, the significance in terms of the p-value of each single trend in each time step is calculated. To do so, 1000 phase surrogates of each single realization’s vegetation residual are created. For each surrogate, the indicators are then calculated in the same manner as for the actual state variable. For each time step, the trend in the surrogate’s as well as original state variable’s indicators until this point in time is measured. The p-value is then defined as the one minus the percentile in which the later is when assuming it results from the distribution given by the former. An indicator at a given time and cell is regarded significant, if p < 0.05. The time of emergence is then defined as the first time when the trend becomes significant. The ToE was similarly defined e.g. in Hawkins and Sutton (2012) as the first time a signal-to-noise ratio is above a certain threshold. An indicator of CSD used as an Early Warning Sign (EWS) should preferably warn as early as possible. Thus, indicators are better when their increase is significant long before a Tipping Point. Furthermore, they are more reliable when the spread in the ToE over the realizations is small.