Table of Links
-
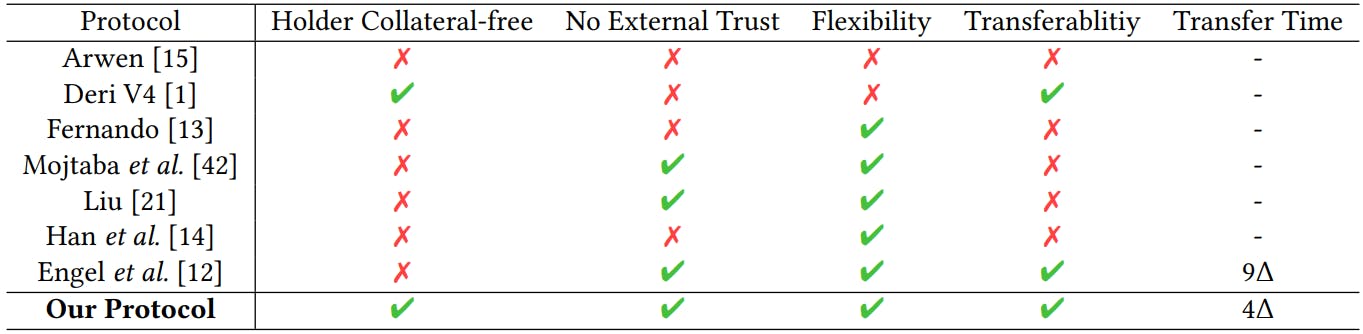
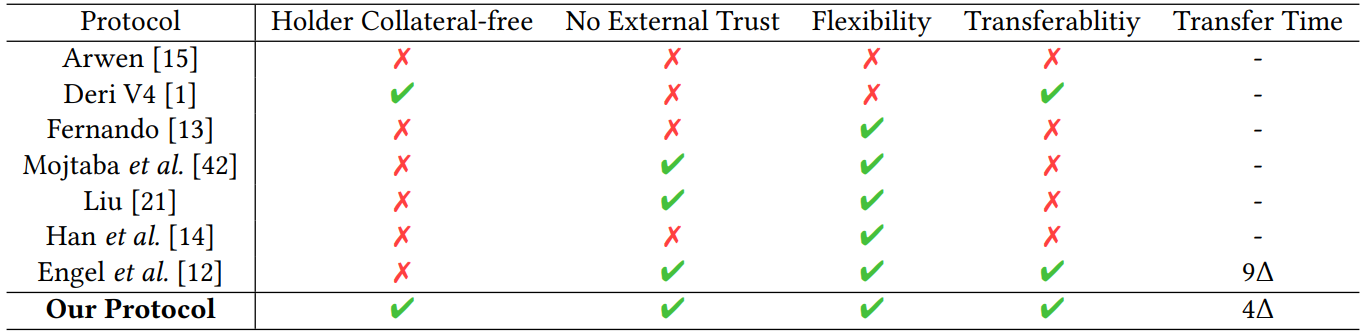
Protocol
-
Security Analysis
A. Codes
B. Proofs
3 OVERVIEW
Consider the scenario described in Section 1: Alice and Bob strike a deal: Bob agrees to sell his 100 guilder coins to Alice in exchange for 100 florin coins within one week. To secure this arrangement, Alice pays a 2-florin premium for the option to complete the transaction. The 100 florin and 100 guilder coins are referred to as 𝐴𝑠𝑠𝑒𝑡𝐴 on 𝐶ℎ𝑎𝑖𝑛𝐴 and 𝐴𝑠𝑠𝑒𝑡𝐵 on 𝐶ℎ𝑎𝑖𝑛𝐵, respectively, with one week as the
expiration time 𝑇𝐸. Suppose there are 𝐿 holder position bidders, 𝐶𝑎𝑟𝑜𝑙𝑖 , and 𝑀 writer position bidders,𝐷𝑎𝑣𝑒𝑗 , where 𝑖 ∈ {1, 2, . . . , 𝐿} and 𝑗 ∈ {1, 2, . . . , 𝑀}. They are willing to pay a holder transfer fee, 𝐻𝑜𝑙𝑑𝑒𝑟𝐹𝑒𝑒𝑖 , and a writer transfer fee, 𝑊 𝑟𝑖𝑡𝑒𝑟𝐹𝑒𝑒 𝑗 , to obtain the option position from Alice and Bob, respectively. The holder transfer fee represents the price for the option and Alice’s asset locked in the contract, while the writer transfer fee is the fee to acquire Bob’s risky asset locked in a contract with obligations tied to that asset. An HTLC-based option requires Alice to escrow 𝐴𝑠𝑠𝑒𝑡𝐴 in advance, followed by Bob escrowing 𝐴𝑠𝑠𝑒𝑡𝐵.
Making transfer more robust and efficient. In an HTLC-based option, Alice and Bob lock their assets with the hashlock 𝐻(𝐴), where 𝐴 is the exercise secret generated by Alice. Consider the case where Carol purchases Alice’s position. In the previous work [12], the protocol first locks the contracts by tentatively assigning a new hashlock to replace the old one. Considering that Alice can place different hashlocks on two chains and Carol may replace Alice on one chain but not the other, Bob is given a time-consuming consistency phase to ensure the new hashlocks are consistent. We would like to reduce the time needed for this transfer.
We manage to reduce the transfer time by a key observation. Since Alice cannot transfer the option to multiple bidders simultaneously, it logically prompts the use of Double-AuthenticationPreventing Signatures (DAPS) to prevent a seller from selling signatures to multiple bidders, thus remove the requirement of guaranteeing consistency by Bob’s efforts. If multiple signatures are revealed, a secret key can be extracted by DAPS, then punishment is enforced automatically to ensure fair payoff. By adopting DAPS, the transaction completion in our protocol is less than half the time of the previous method [12].
Holder Collateral-Free Cross-Chain Options. Our objective is to allow Alice to pay a premium to secure this right, without the need to escrow the assets in advance. We need a mechanism to enable the correct exercise of this right—Alice pays her florin coins to get Bob’s guilder coins. Alice cannot get Bob’s coins without paying florin coins to Bob. A naive approach would be requiring cross-chain transaction confirmation of Alice’s escrow when Alice decides to exercise. However, cross-chain bridges, which are used for cross-chain transaction confirmation, suffer from various security issues [19, 40], such as key leakage [24], smart contract vulnerabilities [28, 37], and rug pulls [18, 38]. We want to design a holder collateral-free option without a trusted cross-chain bridge.
If we grant Alice direct access to the exercise right (or the preimage of hash, exercise secret in HTLC), then Bob’s interests is not protected, as Alice could withdraw Bob’s coins directly. To resolve this problem, we resort to economic incentives that commonly present in the DeFi markets, which are also drive forces for options. We let Bob control the exercise secret while Alice retains the right to penalize Bob. In addition to a collateral (100 guilder coins in our example) required by normal option contracts, we ask Bob to lock another valuable asset on 𝐶ℎ𝑎𝑖𝑛𝐴 as a guarantee for Alice when she wants to exercise the right. If Alice later sends her coins on 𝐶ℎ𝑎𝑖𝑛𝐴 in order to exercise her right but Bob does not release the exercise secret, Alice will get Bob’s guarantee as compensation. Suppose this guarantee is sufficient (even more than sufficient) to compensate the expected profit of this option, this method gives Bob incentives to cooperate when Alice wants to exercise her right. Integration. We then integrate the efficient option transfer protocol into the holder collateral-free cross-chain options. Bob controls the exercise secret and the transfer process instead of Alice, then the processes for transferring the holder and writer are reversed. The hash of exercise secret on both chains must remain identical after Bob transfers his position to Dave. A key challenge is ensuring that honest parties incur no losses. This involves addressing potential misbehavior by any party and collusion between any two parties. To counter these, we introduce a withdrawal delay to allow Dave to retrieve assets in case Bob acts maliciously and a transfer confirmation delay to allow Alice to contest any inconsistent replacement of the hashlock.
Authors:
(1) Zifan Peng, The Hong Kong University of Science and Technology (Guangzhou) Guangzhou, Guangdong, China ([email protected]);
(2) Yingjie Xue, The Hong Kong University of Science and Technology (Guangzhou) Guangzhou, Guangdong, China ([email protected]);
(3) Jingyu Liu, The Hong Kong University of Science and Technology (Guangzhou) Guangzhou, Guangdong, China ([email protected]).
This paper is available on arxiv under CC BY 4.0 license.