This paper is available on arxiv under CC BY 4.0 license.
Authors:
(1) Zhibo Xing, School of Cyberspace Science and Technology, Beijing Institute of Technology, Beijing, China, and the School of Computer Science, The University of Auckland, Auckland, New Zealand;
(2) Zijian Zhang, School of Cyberspace Science and Technology, Beijing Institute of Technology, Beijing, China, and Southeast Institute of Information Technology, Beijing Institute of Technology, Fujian, China;
(3) Jiamou Liu, School of Computer Science, The University of Auckland, Auckland, New Zealand;
(4) Ziang Zhang, School of Cyberspace Science and Technology, Beijing Institute of Technology, Beijing, China;
(5) Meng Li, Key Laboratory of Knowledge Engineering with Big Data (Hefei University of Technology), Ministry of Education; School of Computer Science and Information Engineering, Hefei University of Technology, 230601 Hefei, Anhui, China; Anhui Province Key Laboratory of Industry Safety and Emergency Technology; and Intelligent Interconnected Systems Laboratory of Anhui Province (Hefei University of Technology)
(6) Liehuang Zhu, School of Cyberspace Science and Technology, Beijing Institute of Technology, Beijing, 100081, China;
(7) Giovanni Russello, School of Computer Science, The University of Auckland, Auckland, New Zealand.
TABLE OF LINKS
Zero-Knowledge Proof-Based Verifiable Machine Learning
Existing Scheme & Challenges and Future Research Directions
Conclusion, Acknowledgment and References
II. BACKGROUND
We provide background knowledge on machine learning and zero-knowledge proof, outlining how zero-knowledge proof addresses the verifiability gaps in machine learning.
A. Machine Learning
Machine learning is a potent computational technique designed to learn patterns and knowledge from data, enabling predictions, classifications, and decision-making. While machine learning finds widespread applications across various domains, privacy and security concerns have always been critical aspects of its development. On one hand, model training relies on vast amounts of data, some of which are generated and collected in people’s daily lives. These data contain sensitive and private information, making it imperative to ensure their
privacy [25]. On the other hand, machine learning models themselves may inadvertently leak sensitive information. Attackers can analyze a model’s outputs to gain insights into the training data, potentially compromising privacy [26]. Furthermore, machine learning models are vulnerable to adversarial attacks. Attackers can poison models by carefully crafting specific inputs, significantly reducing their accuracy under certain conditions [27]. To illustrate the application of zeroknowledge proofs in machine learning, we introduce machine learning through key concepts, common models, and working mechanisms.
- Key Concepts: Machine learning is often deemed as a solution to a specific optimization problem. The workflow for solving an optimization problem with machine learning is roughly as follows:
- Design the appropriate model to describe the optimization problem and the corresponding optimization method.
2) Optimize the model by updating parameters according to that optimization method by means of available training dataset.
3) Output the optimal solution by feeding the dataset into the optimized model.
As the problems we aim to address become increasingly complex, the designed models are also growing in size. More complex networks entail a greater number of parameters, leading to higher training costs. These costs stem from both the demand for extensive datasets and substantial computational resources. However, when we need to share the computation results with others, how can we convincingly demonstrate that these results were indeed obtained through honest computation? This gives rise to the issue of verifiability. Yet, due to data privacy concerns or computational limitations, the other party might be unable to verify the results through a step-by step re-calculation process. In such cases, an efficient method is needed that can verify the correctness of computation results without accessing the input data.
2) Common Models: The computational processes in machine learning exhibit certain characteristics. On one hand, the data involved in these computations often take the form of vectors, matrices, or tensors. On the other hand, despite the variety of models and algorithms, they are typically derived from a few mainstream model structures and algorithmic concepts. This commonality in the computational processes of machine learning offers additional possibilities for efficient verification. We introduce several commonly used models and algorithms in machine learning to illustrate their computational characteristics.
For traditional models, we consider linear regression and decision trees. These traditional models are simple in structure and computational process. Linear regression is a fundamental machine learning and statistical modeling method used to establish linear relationship models between variables. The core of a linear regression model lies in analyzing the relationship between independent variables and a dependent variable, typically expressed as y = Σn i=0βixi+ϵ [28]. Various optimization methods can be employed to train the model parameters. For instance, this can be achieved through direct computation using gradient descent algorithms or indirectly by transforming it into a dual problem for computation. Decision tree is a commonly used supervised learning algorithm for classification and regression problems. It relies on a treelike structure of decision rules to classify data and make predictions. By training on data, the model adjusts its structure and parameters, and ultimately generates decision paths based on decision rules in the nodes to make decisions [29]. One of the key features of decision trees, distinguishing them from other machine learning models, is their core computational process based on comparisons. This is because the decision rules in the nodes typically take the form of ”if the value of feature A is less than threshold T, then go to the left sub-tree, otherwise, go to the right sub-tree.”
For deep models, we consider neural networks and convolutional neural networks. In general, deep models require more computational resources during training compared to traditional models. The essence of neural networks is to simulate the behaviour of neurons in the human brain for information processing and transmission [30]. A neural network is a network structure composed of hierarchically arranged neurons, where each neuron typically follows the form Y = W X + b. In this equation, Y represents the neuron’s output, W is the weight matrix containing all the weights connecting the inputs to the neuron, X is the input vector containing all input features, and b is a constant bias term. This structure leads to matrix and vector multiplications being a primary operation in neural networks. Additionally, to enable neurons to learn and capture non-linear relationships in the data, activation functions are introduced. Common nonlinear activation functions include ReLU (y = max(0, x)), Softmax (yi = exp(xi)/Σ n i=0exp(xi)), Sigmoid (y = 1/(1 + exp(−x))), and others [31]. Convolutional neural network primarily focus on two-dimensional data structures and are well-suited for processing images and spatial data. Compared to regular neural networks, the key feature of CNNs is the introduction of convolution operations, allowing them to establish connections within local regions and reduce the number of parameters. Briefly, for matrices X and Y of size m ∗ m and n ∗ n, the convolution Z = X ∗ Y is represented as Zi,j = Pn−1,n−1 k=0,l=0 Xi+k,j+l · Yk,l for i, j = 0, ..., m − n [32]. Obviously, compared to matrix and vector multiplication in neural networks, convolution operations introduce greater computational complexity.
3) Working Mechanisms: To comprehensively enumerate the types of computations involved and the distribution and interaction modes between nodes in machine learning, we take machine learning pipelines, outsourced machine learning, and federated machine learning as examples. We explain the differences in computation types and privacy settings arising from their distinct working mechanisms.
Outsourced machine learning is the fundamental scenario when considering the verifiability of machine learning. Therefore, in this scenario, we primarily focus on the training and inference processes of the model. The workflow in this scenario is illustrated in figure 3(a). In this scenario, based on the given input data, along with the corresponding algorithm and a defined model, computations are performed to obtain
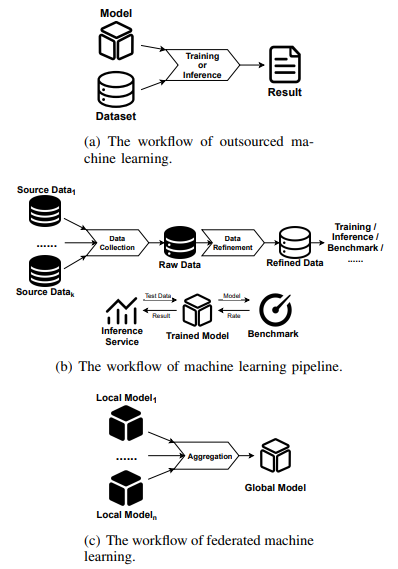
the inference results or updated models. Here we exclude KMeans, DBSCAN and other clustering algorithms that do not have an explicit model concept. When the party requesting the results (requesting party) is not involved in the computation, it becomes necessary for the party responsible for the computation (computing party) to provide the reliability of the final results. Otherwise, the requesting party may be deceived by false results and end up paying computational fees to the computing party. It becomes necessary to demonstrate the statement that ”the result is indeed computed according to the given data and process.” Additionally, for privacy reasons, the computing party does not wish to reveal the private input data used during the verification. There are primarily two types of privacy settings to consider here. One is outsourced training, where the computing party does not possess or only has limited access to privacy inputs (such as training hyperparameters). The other is outsourced inference, where the computing party provides its private model as input. Zero-knowledge proofs are well-suited for tasks where the computational process is complex, yet the interaction is simple. In this case, the computing party needs to provide the aforementioned statement while protecting the confidentiality of certain input data. An intuitive approach is to transform the fixed algorithm into a circuit and then demonstrate the circuit’s satisfiability based on input and output. That is, using zero-knowledge proofs to establish the correctness of the computational process.
In machine learning pipeline, the task of the entire machine learning process, from data pre-processing to model utilization, are assigned to different parties for execution. The data pre-processing phase is often overlooked in discussions of machine learning security. Therefore, in the context of the machine learning pipeline, we primarily focus on the data pre-processing part. In the pipeline, different tasks are assigned to different roles, and data pre-processing is typically divided into two sub-tasks: data collection and data refinement. This allows for a more granular analysis of the verifiability issues within this phase. Data collection refers to the selection and collection of data from various original data owners that meet certain requirements, resulting in the acquisition of a selected dataset. This process often involves interacting with databases and performing relevant operations to extract the desired data. On the other hand, data pre-processing involves applying specific pre-processing algorithms to transform and enhance the features of the data, aiming to improve the quality of the data. Specifically, the additional workflow of an ML pipeline is illustrated in figure 3(b). When different parties are responsible for different tasks, it becomes necessary to provide proofs of correctness to subsequent parties regarding the results they provide. Meanwhile, due to privacy concerns, these parties also do not want to disclose any additional information about the original inputs during the verification process. In this case, the data collecting party needs to provide proof to the data refining party that ”the given dataset is indeed obtained through the specified collecting steps from these original dataset”. Meanwhile, the data refining party needs to prove to the data consumers that ”the given data is indeed obtained through the specified pre-processing algorithm”. Unfortunately, it is rare for these two operations to be combined with zero-knowledge proofs to prove their correctness. The former operation, involving database operations, is often associated with the concept of Verifiable Database (VDB) [33]. Database operations are not computationally intensive but rather involve high input-output complexity, which poses challenges for integrating zero-knowledge proofs. Existing VDB solutions often employ lightweight techniques such as digital signatures [34], polynomial commitment [35], TEE [36], etc., to improve the efficiency. From the perspective of ZKP, Singh et al. [37] designed a zero-knowledge proof schemes for operations such as aggregation, filtering within the context of ML pipelines. As for the pre-processing algorithms, there is limited effort dedicated to treating them as seperate computations and designing verification schemes to ensure the correctness. Only Wang et al. designed the ezDPS [38] scheme to prove the correctness of DWT and PCA data processing algorithms in the ML pipeline scenario.
The rise of federated machine learning can be attributed to its effective utilization of edge computing power and its commitment to preserving user data privacy. In federated learning, participants contribute to the updates of the global model by providing the local model trained with their own local data. The contribution of individual participants’ data to the performance improvement of the global model through model aggregation is crucial, as depicted in figure 3(c). In this scenario, based on several local models, along with the given aggregation rule, computations are performed to obtain the updated global model. Here, we consider the client-server model, where the computation of the aggregation process is handled by a central server. In order to protect against data reconstruction attacks and potential privacy breaches by malicious servers, the server needs to provide proof of the correctness of global model aggregation to the client. Additionally, in certain privacy settings, the server also needs to safeguard the local models contributed by each client. Zero-knowledge proofs, in terms of functionality, can address the aforementioned issues. As demonstrated by Xu et al. in VerifyNet [39], they constructed a zero-knowledge proof scheme based on bilinear pairings, which achieved the verification of global model aggregation integrity while preserving the privacy of local models. However, Guo et al. pointed out that VerifyNet incurred significant communication overhead due to the use of zero-knowledge proofs. As an alternative, they proposed VeriFL [40], which employs simpler hash and commitment schemes. Additionally, Peng et al. introduced VFChain [41], which addresses this issue through the utilization of blockchain and consensus protocols. The computations involved in model aggregation are relatively simple and fixed, and as a result, zero-knowledge proofs, as a general-purpose proof scheme, do not offer performance advantages in such tasks.
B. Zero-Knowledge Proof
We introduce the definition, common used schemes, and illustration of the advantages of zero-knowledge proof over other cryptographic techniques in terms of machine learning verifiability.
1) Definition: Zero-knowledge proof (ZKP) [42] is proposed as a two-party cryptographic protocol running between a prover and a verifier for proving a statement without revealing anything else. In simple terms, zero-knowledge proofs possess the following three properties:
• Completeness: Given a statement of a witness, the prover can convince the verifier that the statement is correct if the protocol is executed honestly.
• Soundness: Any malicious prover cannot fool the verifier into accepting a false statement.
• Zero-Knowledge: The prover does not leak any information else but the correctness of the statement during the protocol.
For the more commonly used non-interactive zero-knowledge proof schemes in the ZKP-VML scenario, we provide their formal definition as follows:
Let R be a relation generator that given a security parameter λ in binary returns a polynomial time decidable binary relation R. For pairs (ϕ, w) ∈ R, we call ϕ the statement and w the witness. We define Rλ to be the set of possible relation R may output given 1 λ . An efficient prover publicly verifiable non-interactive argument for R is a quadruple of probabilistic polynomial algorithms (Setup,Prove, Vfy, Sim) such that
• (σ, τ ) ← Setup(R) : The setup take a security parameter λ and a relation R ∈ Rλ as input, outputs a common reference string σ and a simulation trapdoor τ for the relation R. The algorithm serves as an initialization for the circuit and needs to be executed only once for the same circuit.
• π ← Prove(R, σ, ϕ, w) : The prove take a common reference string σ and (ϕ, w) ∈ R as input, outputs argument π.
• 0/1 ← Vfy(R, σ, ϕ, π) : The vfy takes a common reference string σ, a statement ϕ and an argument π as input, outputs 0 (reject) or 1 (accept).
• π ← Sim(R, τ, ϕ) : The sim takes a simulation trapdoor τ and statement ϕ as input, outputs an argument π.
Definition 1: We say (Setup, Prove, Vfy, Sim) is a noninteractive zero-knowledge argument of knowledge for R if it has perfect completeness, computational soundness and computational knowledge soundness as defined below.
Perfect completeness says that, given any true statement, an honest prover should be able to convince an honest verifier. For all λ ∈ N, R ∈ Rλ,(ϕ, w) ∈ R:
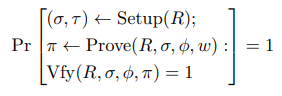
Computational soundness says that it is not possible to prove a false statement. Let LR be the language consisting of statements for which there exist matching witnesses in R. Formally, we require that for all non-uniform polynomial time adversaries A:

Computational knowledge soundness says that there is an extractor that can compute a witness whenever the adversary produces a valid argument. Formally, we require that for all non-uniform polynomial time adversaries A there exists a nonuniform polynomial time extractor XA such that:

2) Common schemes: We present six common technical paths for constructing zero-knowledge proof schemes especially those related to verifiable machine learning.
Sumcheck protocol [43] is an interactive protocol to sum a multivariate polynomial f : F P ℓ → F with binary inputs: b1,b2,...,bℓ∈0,1 f(b1, b2, ..., bℓ). Directly summing requires 2 ℓ computations according to the combinations of bi . To be able to prove the computational process of the polynomial to the verifier V efficiently, prover P can generate a proof of size O(dl), where d is the variable-degree of f, via the sumcheck protocol.
In the sumcheck protocol, the prover P eventually needs to expose the polynomial in order for the verifier V to evaluate at two challenge points, which results in it not being zero-knowledge. By applying a zero-knowledge polynomial commitment following the framework in [44], the polynomial can be concealed and zero-knowledge can be achieved. Furthermore, the interactive challenge process can be replaced by the Fiat-Shamir transformation [45], and the sumcheck thus become a non-interactive, zero-knowledge proof protocol.
Quadratic arithmetic program (QAP) [46] is an effective coding method of circuit satisfaction (C-SAT), by which the CSAT problem can be reduced to divisibility problem between polynomials.
Definition 2: A quadratic arithmetic program Q converted from arithmetic circuit C in field F is consisting of three sets of polynomials ui(x), vi(x), wi(x) m i=0 and a target polynomial t(x). For public inputs and outputs (c1, ..., cl), the Q is satisfiable if and only if there exist coefficients (cl+1, ..., cm) such that t(x) divides p(x), where p(x) = (Pm i=1 ci · ui(x)) · ( Pm i=1 ci · vi(x)) − Pm i=1 ci · wi(x).
Based on the QAP and the common reference string (CRS) model [47], Gennaro et al. [46] constructed zero-knowledge succinct non-interactive argument of knowledge (zk-SNARK).
Inner product argument (IPA) [48] is an interactive protocol to prove the knowledge of the inner product of vectors a, b such that A = g a , B = h b, z = a·b, given z, A, B, g, h. The core idea of IPA is to recursively reduce the length of the vector up to the scalar by random challenges. In order to construct a zero-knowledge proof from IPA, the arithmetic circuit constraints between and among multiplication gates are first formalized by the Schwartz-Zippel Lemma [49], [50] as the problem where the coefficients of particular terms in a polynomial are zero. And then transformed into a statement of inner product form, which can be handled by IPA directly.
MPC-in-the-head [51] is an approach to constructing zero-knowledge proofs via secure multi-party computation (MPC) protocols.
Definition 3: A secure multi-party computation (MPC) protocol Πf allows n participants P1, ..., Pn to compute a common output y = f(x, w1, r1, ...) based on the common input x, respective secret input w1, ..., wn and random inputs r1, ..., rn through k rounds of interaction processes. Let the view of participant Pi be Vi = (x, wi , ri , Mi), where Mi = (mi,1, ..., mi,k) denotes the message received by Pi . Then the behavior of participant Pi can be determined by the number of rounds j and the current view Vi,j = (x, wi , ri ,(mi,1, ..., mi,j )).
The prover simulates several participants to executes a multi-party computation protocol and saves the views of each participant in the process. The verifier checks these views through commitments to verify the correctness of the protocol execution process.
3) Advantages of zero-knowledge proof: For the verifiable computation in machine learning, zero-knowledge proof can not only prove the integrity of the computation process, but also avoid revealing any additional information during the verification. There are several cryptographic techniques that can solve the problem to varying degrees, but there are also some drawbacks.
Secure multi-party computation (SMC) is a cryptographic technology that enables parties to jointly compute a determined function without revealing their private inputs [52]. However, SMC relies on-synchronised communication between parties, and most of which do not support dynamic joining or exiting of users. Compared to SMC, zero-knowledge proof is, or can be easily converted (by a Fiat-Shamir transformation [45]) into, a non-interactive protocol. This asynchronous support is important considering factors such as the different training paces of each parties.
Homomorphic Encryption (HE) is a cryptographic technology that enables any third party to operate on the encrypted data without decrypting it in advance [53]. According to the operation allowed, the HE scheme can neatly be categorized as Partially Homomorphic Encryption (PHE) and Fully Homomorphic Encryption (FHE). But PHE can only support a specific operation on ciphertext (e.g. addition), which has difficulty in covering a wide range of operations in the machine learning process. FHE, on the other hand, can support a variety of operations, but it is extremely expensive, especially for computationally intensive applications such as machine learning. Compared to HE, ZKP is more efficient for processing massive computation. Efficiency is as important as usability for verifiable machine learning.
Differential privacy (DP) is a cryprtographic technology that enables the privacy protection of a single item in the database while having almost no effect on the statistical results of the database [54]. Unfortunately, although DP has formally provable privacy, it contributes nothing to verifiability. Compared to DP, ZKP protects the privacy through its zero-knowledge properties, and the computational process can be verified by proofs
Trusted execution enviornments (TEE) is a cryprtographic technology that guarantees the authenticity and confidentiality of the code execution process through an isolated hardware environment [55]. While both TEE and ZKP guarantee the correctness and privacy of the learning process, TEE on the one hand has to rely on a trusted hardware service provider for its security. On the other hand, as a cryptographic technology based on a hardware environment, it inevitably introduces additional implementation costs. Compared to TEE, the security of ZKP relies on provable cryptographic assumptions and, as a protocol, its implementation does not introduce additional costs.