This paper is available on arxiv under CC BY 4.0 license.
Authors:
(1) Zhibo Xing, School of Cyberspace Science and Technology, Beijing Institute of Technology, Beijing, China, and the School of Computer Science, The University of Auckland, Auckland, New Zealand;
(2) Zijian Zhang, School of Cyberspace Science and Technology, Beijing Institute of Technology, Beijing, China, and Southeast Institute of Information Technology, Beijing Institute of Technology, Fujian, China;
(3) Jiamou Liu, School of Computer Science, The University of Auckland, Auckland, New Zealand;
(4) Ziang Zhang, School of Cyberspace Science and Technology, Beijing Institute of Technology, Beijing, China;
(5) Meng Li, Key Laboratory of Knowledge Engineering with Big Data (Hefei University of Technology), Ministry of Education; School of Computer Science and Information Engineering, Hefei University of Technology, 230601 Hefei, Anhui, China; Anhui Province Key Laboratory of Industry Safety and Emergency Technology; and Intelligent Interconnected Systems Laboratory of Anhui Province (Hefei University of Technology)
(6) Liehuang Zhu, School of Cyberspace Science and Technology, Beijing Institute of Technology, Beijing, 100081, China;
(7) Giovanni Russello, School of Computer Science, The University of Auckland, Auckland, New Zealand.
TABLE OF LINKS
Zero-Knowledge Proof-Based Verifiable Machine Learning
Existing Scheme & Challenges and Future Research Directions
Conclusion, Acknowledgment and References
III. ZERO-KNOWLEDGE PROOF-BASED VERIFIABLE MACHINE LEARNING
A. Definition
We model zero-knowledge proof-based verifiable machine learning through participants, algorithms, and workflows.
There are two types of participants, namely verifier V and prover P. Since V does not have enough computing power or data, V needs to delegate some machine learning tasks (training or inference) to P. So the main bulk of the computations involved in the machine learning are performed by the prover P, and further verified by V that whether all these computations are performed correctly. Depending on different tasks and privacy settings, the two participants may possess different data and objectives. Neither of these participants is honest, they will try to steal private data from other, which may lead to privacy compromise to the data owner. And the prover P may further performs the computation dishonestly (e.g. learning with incorrect data, or directly generating a well-formed learning result), which can cause a severe impact on the learning task.
Gennaro [56] provided a formal definition of outsourced computation with four algorithms. In order to provide an accurate and unambiguous description, we define the noninteractive verifiable machine learning modeled after that.
Definition 4: A zero-knowledge proof-based verifiable machine learning allowing a prover P to trustfully execute given machine learning task T with specific input data D for verifier V is a tuple of below algorithms:
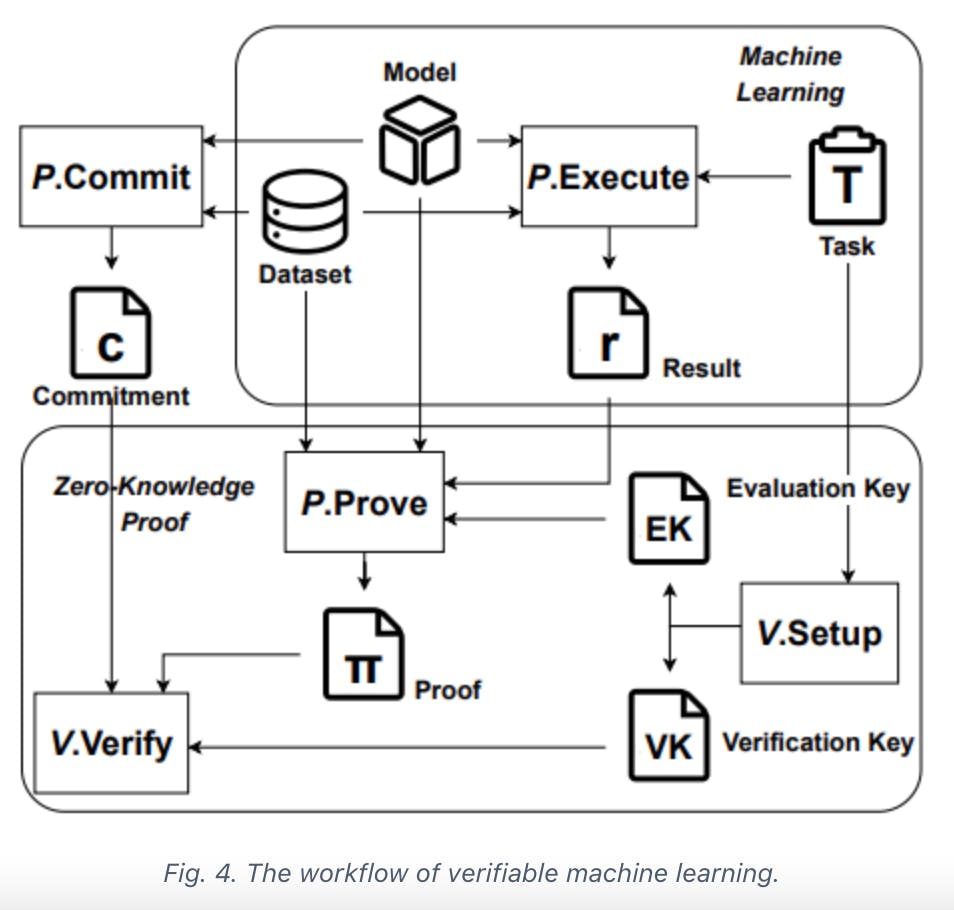
• (PK, V K, T D) ← Setup(T, λ): By inputting the task T and a security parameter λ, the algorithm generates an prover key PK for the prover P to generate the proof. And a verifier key V K for the verifier V to verify the proof.
• c ← Commit(PK, DP ) : By inputting the input data D, the algorithm generates the commitment c for those inputs that need to be hidden.
• r ← Execute(T, DP , DV ) : By inputting the task T and input data D, the algorithm perform the task T and outputs the execution result r (varies depending on the task, maybe a prediction or parameters).
• π ← Prove(PK, DP , DV , r) : By inputting the evaluation key EKT , input data D and result r, the algorithm generates the corresponding proof π for the execution process.
• {0, 1} ← Verify(V K, π, c, r, DV ) : By inputting the verification key V KT , proof π and commitment c, the algorithm checks whether the committed inputs are used for execution with c and π. And whether the execution process is correct with π and V KT . If the verification pass, the algorithm outputs 1, otherwise 0.
• π ← Sim(T D, c, r, DV ) : By inputting the trapdoor T D and a result r, the algorithm generates the corresponding proof π.
The workflow of verifiable machine learning is shown in Figure 4. Both parties agree on the machine learning task T and input data D(including the dataset, model, auxiliary input, etc.). After receiving the commitment c of input data D from prover P generated with Commit, verifier V runs Setup to generate keys for proving and verifying. Prover P performs the machine learning task with Execute to acquire the result r. During which the proof π is also generated by Prover P with Prove. Finally, with the execute result r and corresponding proof π, V can verifies whether P execute the machine learning task T correctly through Verify. If proof π pass the verification, then V is convinced that P has faithfully executed the machine learning task T to obtain the result r with input data D, otherwise, V rejects the result.
And we give several basic properties for this scheme to meet:
• Completeness. If P has honestly completed the task with the given input, then Verify outputs 1 (Accept) with the
probability of 1.

• Soundness. If P is malicious then Verify outputs 1 with a negligible probability. For any PPT adversary A,

• Zero-knowledge. If the scheme leaks no information about the prover’s private input DP besides the verification result to V.

If one scheme meets completeness and soundness, then it is a verifiable scheme. A verifiable scheme is mostly used in outsourced training scenarios, where V sends the model M and the training dataset D to P. Thus, the scheme only needs to focus on efficient proof generation and verification
and does not necessarily require zero-knowledge properties, as the verifier V already possesses knowledge of the input. And if the scheme can only guarantee 1) the correctness of the result rather than the execution process or 2) the correctness of the process according to some proportion, then the verifiability is only partially satisfied. For the former, these scheme can only ensure that the results appear to be correct but may not fundamentally guarantee the reliability of the computation process. Malicious participants could potentially resubmit certain computation results and their corresponding proofs that pass verification, thereby reducing their computational costs. Regarding the latter, although it can mitigate poisoning attacks to some extent, it still has certain security vulnerabilities when considering malicious behavior that directly alters computation results in individual rounds.
A zero-knowledge verifiable scheme can protect the proverprivate input, for V knows nothing more than the verification result during the scheme. This approach finds widespread utility in scenarios such as federated learning, which places a strong emphasis on preserving the privacy of training data. Federated learning is designed to protect the privacy of data providers, but this very aspect can make it challenging to audit the training process. This scheme not only ensures the trustworthiness of the training results but also preserves the privacy protection attributes inherent to federated learning.
In addition, considering existing work, we also need to discuss another scenario, which is auditability. Auditability refers to the ability of a verifier to confirm that the data used by the prover is indeed the data they previously committed to, i.e., the verification of the commitment c. While this should be considered as a fundamental property of ZKP-VML schemes, its importance is equivalent to verifiability. Otherwise, the verification would focus solely on the effort expended rather than ensuring coherent correctness. However, given that a few schemes overlook this aspect, where they only verify the computation process and lack constraints on input data, it is also raised as one of the evaluation criteria.
B. Challenges
We clarify the challenges that a ZKP-based verifiable machine learning scheme faces.
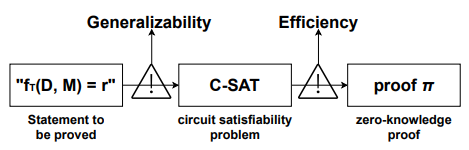
Based on the workflow mentioned above, to prove the correctness of some computational process, an intuitive idea is to transform the task T into a single algorithm fT and then prove the statement fT (D, M) = r by a zero-knowledge proof scheme, as shown in figure 5. Unfortunately, most of machine learning algorithms are too complex and large for existing zero-knowledge proof schemes, making the proof generation and verification impossible. Specifically, there are two main challenges.
The first challenge is generalizability. Due to the nature of sample data, learning parameters, etc., the vast majority of computations involved in machine learning are floating-point computations. However, as a cryptographic technique, zero-knowledge proof works on groups of finite fields. Therefore, the statement containing the floating-point computation process cannot be directly translated into the circuit satisfiability problem expressed with elements over a finite field. This is just one of the issues that arise when transitioning between zero-knowledge proofs and machine learning. Other issues include but are not limited to representing computation processes beyond addition and multiplication, arithmeticizing towards different circuit representations, and so on.
The second challenge is efficiency. On one hand, considering the complexity of the machine learning computation process, designing a specialized proof system is particularly challenging, and there are currently no such schemes available. On the other hand, the efficiency of general proof systems is often insufficient for practical needs in this scenario. Consider some general-purpose zero-knowledge proof systems, such as Groth16, one of the most commonly used zk-SNARK scheme. The computational complexity of its proof generation is O(|C|)E. |C| denotes the size of the arithmetic circuit, which is directly related to the amount of computation involved, and E denotes the exponentiation in groups. It is unaffordable to apply a computationally intensive task like machine learning to zero-knowledge proofs. For a specific model VGG16[57], the proof generation time reaches a staggering 10 years. Also the size of the generated evaluation key and verification key exceeds 1,000 TB, which also requires an enormous amount of memory to handle. How to prove the computational process of machine learning efficiently has also become a pressing problem.